Measuring Language – II

Recently, a member of the Department of Psychology at the University of Auckland in New Zealand, Dr Quentin D. Atkinson, published an article discussing some results of his in one of his principal fields of interest: “Evolution of language, religion, sustainability and large-scale cooperation, and the human expansion from Africa”1.  The data that he worked with indicates that language among humans began once in Africa, and from there spread with the spread of humans across the world, fracturing into about six thousand languages.

The idea that all languages sprang from a single language is not really a new idea:

Genesis 11

1. And the whole earth was of one language and of one speech.

2. And it came to pass, as they journeyed from the east, that they found a plain in the land of Shi-nar; and they dwelt there.

3. And they said one to another, Go to, let us make brick, and burn them thoroughly.  And they had brick for stone, and slime had they for morter.

4. And they said, Go to, let us build us a city and a tower, whose top may reach unto heaven; and let us make us a name, lest we be scattered abroad upon the face of the whole earth.

5. And the Lord came down to see the city and the tower, which the children of men builded.

6. And the Lord said, Behold, the people is one, and they have all one language; and this they begin to do: and nothing will be restrained from them, which they have imagined to do.

7. Go to, let us go down, and there confound their language, that they may not understand one another’s speech.

8. So the Lord scattered them abroad from thence upon the face of all the earth: and they left off to build the city.

9. Therefore is the name of it called Babel; because the Lord did there confound the language of all the earth: and from thence did the Lord scatter them abroad upon the face of all the earth.

Holy Bible, King James version, Genesis, Ch. 11

I am not a biblical scholar, nor much of a believer as well, so when I notice a few gaps in the narrative which have doubtlessly been explained by scholars and believers, I try to ignore them.  I just wonder who the Lord is talking to (angels, seraphim, cherubs, others?) in verse 6 and 7, using the collective pronoun – “let us go down, and there confound their language” – and then wonder why only the Lord is mentioned in the acts of scattering and confounding.  Oh, well, I believe it’s destined to remain yet another mystery.

Linguists appear to have proceeded in exactly the opposite direction: from the fact that there are many different languages, with different word orders, grammars, sounds, etc., sufficient commonalities have been found to enable the classification of languages into families.  The great unification of languages from India with languages from Europe, attributed to Sir William Jones in 1786, though some of the scholarship that enabled that discovery was begun somewhat earlier by others, found that a substantial number of languages derived from a single root: the proto-Indo-European language.

Since then, other language families have been described, though not without controversy.  The linguists can trace various kinds of changes, from sound changes to case-ending changes to word order changes.  They look at meanings: a word that means something in one language is compared to the word that means the same thing in another, and the common sounds can be used to define their relationship.  Their work is brilliant and difficult – having tried to learn a few languages other than English lets me make that statement, since I have been spectacularly unsuccessful.  Eh bien.

In the last century, work has proceeded on the unification of languages into families, but, according The First Word, by Christine Kenneally:

…the search for the origins of language was formally banned from the ivory tower in the nineteenth century and was considered disreputable for more than a century.  The explanation given to me in a lecture hall in late-twentieth-century Australia had been handed down from teacher to student for the most part unchallenged since 1866, when the Societe de Linguistique of Paris declared a moratorium on the topic.  These learned gentlemen decreed that seeking the origins of language was a futile endeavor because it was impossible to prove how it came about.  Publication on the subject was banned.[2]

The work of linguists has been to look at relationships between languages and tried to establish which were related to which.  After the ban is described by Ms. Kenneally:

…most linguists were field linguists, researchers who journeyed into uncharted territory and broke bread with the inhabitants.  They had no dictionary or phrase book but learned the local language, working out how verbs connect with objects and subjects, and how all types of meaning are conveyed. … When they transcribe a language for the first time, they create a rigorous catalog of sounds, words and parts of speech, called the grammar of the language.  Once this is completed they match one catalog to another – finding evidence of family relationships between languages.  Grammar writers are meticulous and diligent, arranging and rearranging the specimens of language into a lucid system.[3]

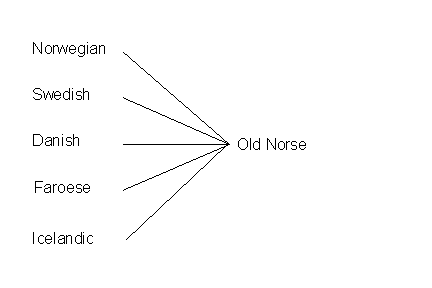
Once the relationships were established, then the language from which the related languages came from could potentially be described, and the relationships could be mapped in tree diagrams.  An example of the kind of tree diagrams that results from this work is below, showing the current languages that appear to have come from a common, older source:

The attempt has been made to take the tree diagrams from existing languages back to earlier languages, but since the 1866 declaration in Paris, the work of linguists has been oriented toward explanations of the trees and grouping of families, without speculating on the original mother language, at least publicly.  Until the late 1950s and early 1960s, that is, at which point, Noam Chomsky made all linguists rethink their methodology with his universal transformative grammar ideas which provided a way to think about all languages as if they were a product a similar way of constructing meaning.  Chomsky himself, however, discouraged the idea of looking at language from an evolutionary standpoint.  A statement of his, quoted in The First Word, is “…that it is ‘hard to imagine a course of selection that could have resulted in language.'”[4]

There have been workers in linguistic analysis who have focused on understanding languages of non-human species – chimps, apes and parrots, with some of their successes contributing to the character of language, its limits and requirements.  Others have looked at the physiological basis for producing language: one notable controversy has been whether or not Neanderthals were physiologically equipped to produce the sounds that would have been used for language by their contemporaries, the Cro-Magnons, and the subsequent Homo Sapiens.  Some others have focused on the neurological basis of language production, notably in mapping the brain and trying to understand how the brain and its assemblage of neurons actually matches sounds to meanings.

Those who have been cataloging languages have developed a set of resources which now reside online, one facet of which is a database of all the sounds produced in all of the languages that have been catalogued, called “The World Atlas of Language Structures” (see below).

But, until 1990, when Stephen Pinker and Paul Bloom published a paper suggesting that the study of the evolution of language was not only possible but necessary, the door to publication of language evolution ideas was closed, and along with it, the door to speculation on “the mother language”.  After the paper, all sorts of approaches were ‘legitimized’, although not without controversies.

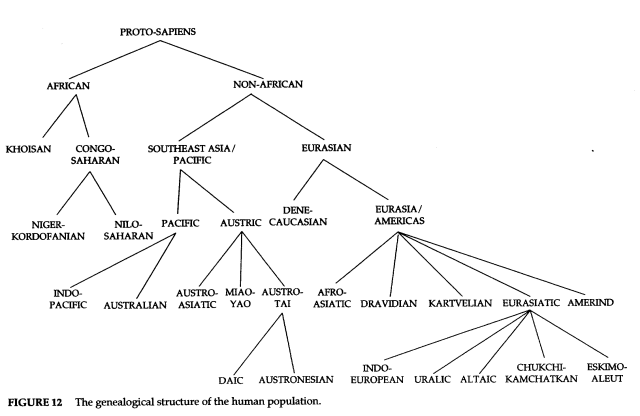
One of the controversial hypotheses was that developed by Merritt Ruhlen, who published a book in 1994 called The Origin of Language.  He built a case for a single origin of human development, and created a tree diagram to show the relationships stemming from the original humans.  His tree parallels the way that he presents language as possibly having developed.

In the book, though, he caveats this diagram as not being “…immune from change as the investigation of human prehistory proceeds.”[5]

Meanwhile, the classical linguists continued to perform the yeoman’s work of trying to develop grammars of all the languages on earth – which are evidently disappearing at an alarming rate.  As a repository for this kind of information, an online database has been developed:

The World Atlas of Language Structures (WALS) is a large database of structural (phonological, grammatical, lexical) properties of languages gathered from descriptive materials (such as reference grammars) by a team of 55 authors (many of them the leading authorities on the subject).

…

WALS Online is a joint effort of the Max Planck Institute for Evolutionary Anthropology and the Max Planck Digital Library.[6]

WALS currently has datapoints for 2678 of the approximately 6000 languages in the world.

Crunching data from databases to derive information is an activity that has become ubiquitous and problematical – there is so much data available in so many different fields that suitable means for crunching it all remains an unfulfilled quest in most of those fields.  In Volume 331 of SCIENCE, 11 February 2011, there is a special section with almost 20 articles about the current surfeit of data.

Dr. Atkinson appears to have cut the gordion knot of the language problem by looking at WALS, selecting a global sample of 504 languages, and counting the number of phonemes in each without trying to match the sounds or sound changes.  Then he related the languages and their number of phonemes to geographical distribution and found that the languages with the largest number of phonemes were in Africa, and that the number of phonemes per language fell off the further from Africa humans appear to have migrated.  The languages with the smallest number of phonemes were found in South America and Oceania.  This pattern is similar to that which Merritt Ruhlen described (see above).

This matches closely with the serial founder effect that has been used to explain the distribution of gene diversity, work done by, among others, Luigi Luca Cavelli-Sforza, described in his book, Genes, Peoples, and Languages, published in 2000: the greatest genetic diversity is found in Africa, and diminishes in a similar pattern the further from Africa one looks.  The “serial founder effect” is based on the idea that the core origin population will have sufficient time and members for its genetic makeup to diversify, while small populations that leave the core population will take with them only a subset of those genes, and even as it grows, will have had fewer members and less time to diversify.  And if one of those smaller populations splits, the “serial” effect occurs in that the split will provide another genetic bottleneck.

I have not followed the articles subsequent to Dr. Atkinson’s, in which I expect very smart linguists, geneticists, and psychologists may have pointed out inconsistencies or taken issue with his methodology.  I found his article to be a model of clarity, however, and while I still have doubts, they are hardly informed ones.  I was impressed, though, with his method, which was to take a set of data that no one had looked at in quite the way that he had, and was able to come up with clever measures that gave a new way to reach a conclusion and support an hypothesis.  His analysis is persuasive.

As an aside, when the article in the New York Times appeared describing Dr. Atkinson’s article and work, there was a long thread of reactions to his hypothesis, many of which would have benefited from having actually read Dr. Atkinson’s article before delivering an apparently knee-jerk reaction.  And while I have just covered the surface of this, the books that I have mentioned and the article in SCIENCE are worth the effort to read and comprehend, in understanding the measurement and analysis of language.

The article and books referred to:

Atkinson, Quentin D., “Phonemic Diversity Supports a Serial Founder Effect Model of Language Expansion from Africa”, SCIENCE, 15 April 2011, Vol 332, no. 6027 pp. 346-349, plus online supporting material at

www.sciencemag.org/cgi/content/full/332/6027/346/DC1

Cavalli-Sforza, Luigi Luca, Genes, Peoples, and Languages, translated by Mark Seielstad, University of California Press, Berkeley, CA, 2000.

Kenneally, Christine, The First Word: The Search for the Origins of Language, Penguin Books, New York, N.Y., 2007.

Ruhlen, Merritt, The Origin of Language, Tracing the Evolution of the Mother Tongue, John Wiley & Sons, Inc., New York, N.Y., 1994.

And of course,

Holy Bible, King James version, Genesis, Ch. 11, National Bible Press, Philadelphia, PA, copyright 1958, originally published 1611 in London, England.

---

1 http://www.psych.auckland.ac.nz/uoa/home/about/our-staff/academic-staff

[2] Kenneally, Christine, The First Word: The Search for the Origins of Language, Penguin Books, New York, N.Y., 2007. p. 7.

[3] Ibid, p.26.

[4] Ibid, p.39.  From the  text in The First Word, it is not clear where Chomsky’s quote has come from.

[5] Ruhlen, Merritt, The Origin of Language, Tracing the Evolution of the Mother Tongue, John Wiley & Sons, Inc., New York, N.Y., 1994. Diagram on p 192, statement on p. 193.

[6] http://wals.info/

Measuring Language – I

I stumbled upon a book that I enjoyed enormously, called The Horse The Wheel and Language, How Bronze-Age Riders from the Eurasian Steppes shaped the Modern World, by David W. Anthony, published by Princeton University Press in 2007.  After reading it, I found a review of it in the New York Times from 2008  which I missed when it was originally written.  The review is by Christine Kenneally, the author of the book, The First Word, which was discussed in the post, A Second Look Back – Part 1.  Her review is at:

http://www.nytimes.com/2008/03/02/books/review/Kenneally-t.html

Ms Kenneally has a limited amount of space, but summarizes the 553 pages quite nicely in 10 paragraphs, the last of which reads:

“The Horse, the Wheel, and Language” brings together the work of historical linguists and archaeologists, researchers who have traditionally been suspicious of one another’s methods.  Though parts of the book will be penetrable only by scholars, it lays out in intricate detail the complicated genealogy of history’s most successful language.”1

This most successful language is the Indo-European family of languages.

I don’t remember how I found Dr. Anthony’s book, but after I purchased it as an electronic book and discovered how dense it was, I had to return to my medium of choice, a book, to fully absorb the info.

A substantial portion of Dr. Anthony’s book is devoted to detailed descriptions of the discoveries and excavations in the steppes of Russia, and other discoveries in eastern Europe, some of which were apparently not available due to Iron Curtain politics until after the early 1990s, and also the results of archeological work subsequent to that time.  He provides a chronology of the sites that have been excavated, showing not only the progression of when people lived there, but how they related to their domestic animals: eating them, maintaining them for their wool or milk, using them to draw wagons, using them as sacrifices associated with grave-sites.  He provides details of the discoveries that support his thesis: proto-Indo-European, which preceded and led to Indo-European languages, was developed in the steppes by horse-back riding and wagon- and chariot-building groups that then spread their language both east to Iran and India, and west to Europe.

He also reviews the reconstructions, by linguists, of words that would have been part of proto-Indo-European to provide insight into the objects that were named, and thus are evidence of the content of the lives of the steppe dwellers.  I’ll talk about the linguistic reconstructions later in this post.

By developing a chronology of the settlements that matches a progression from bones of horses with cut marks, as in butchering them for meat, to bones of horses buried apparently ceremonially in the graves of warriors, Dr. Anthony is able to give a time frame during which the change from non-domesticated to domesticated horses likely occurred.

Steppe means “wasteland” in the language of the Russian agricultural state.  The steppes resembled the prairies of North America – a monotonous sea of grass framed under a huge, dramatic sky.  A continuous belt of steppes extends from eastern Europe on the west (the belt ends between Odessa and Bucharest) to the Great Wall of China on the east, an arid corridor running seven thousand kilometers across the center of the Eurasian continent.  This enormous grassland was an effective barrier to the transmission of ideas and technologies for thousands of years.  Like the North American prairie, it was an unfriendly environment for people traveling on foot.  And just as in North America, the key that opened the grasslands was the horse, combined in the Eurasian steppes with domesticated grazing animals – sheep and cattle- to process the grass and turn it into useful products for humans.  Eventually people who rode horses and herded cattle and sheep acquired the wheel, and were then able to follow their herds almost anywhere, using heavy wagons to carry their tents and supplies.2         

One of the questions that Dr. Anthony addresses, and maybe answers, is when did humans begin to use horses for something other than meat.  He reviews the physiological changes that some other species have undergone when domesticated and cites some similar changes in horses.  Bone structure appears to change, and depending on why animals are domesticated, for food (meat), for milk, for wool, etc., changes are generally regular.  Then, he builds a case for the answer being found by careful measurement of the wear on certain of the teeth in horses: his hypothesis being that bit wear might show the difference between domesticated horses and non-domesticated horses.

There is the one use for horses as domesticated animals that is nearly unique: they are ridden or put to pulling wagons, chariots, etc. that require the humans using them to be able to control them.  This is generally done with a “bit”, an apparatus that sits behind the last teeth (designated P₂) and by pulling on one or the other side, affects the soft corners of the mouth of the horse, giving the human pulling on it the ability to signal what he or she wants.  Horses that have metal bits will generally try to move them forward into their teeth to relieve the pain or pressure.   Whether the horses try to push the bit forward or just endure the presence of a bit, there is distinctive wear on the back four teeth, the upper back two and the lower back two, that can be discerned.  The difference in the wear patterns between modern domestic horse teeth ridden with a metal bit and a modern feral horse with no bit use is clear and easy to see.

Dr. Anthony conducted an experiment to understand the wear patterns, and did so in a very methodical way, to accommodate the fact that early horse riders would not have used metal bits.  He had four horses raised and fed in a manner that reflected the likely way that steppe horses of several thousand years ago would have been fed.  Then,

…[e]ach horse was ridden with a different organic bit – leather, horsehair rope, hemp, or bone – for 150 hours, or 600 hours of riding for all four horses.  The horse with the horsehair rope bit was bitted by tying the rope around its lower jaw in the classic “war bridle” of the Plains Indians, yet it was still able to loosen the loop with its tongue and chew the rope.  The other horses’ bits were kept in place by antler cheek-pieces made with flint tools.  At four intervals each horse was anaesthetized by a bemused veterinarian, and we…made molds of its P₂s.  We tracked the progress of bit wear over time, and noted the differences between the wear made by the bone bit (hard) and the leather and rope bits (soft). 

The riding experiment demonstrated that soft bits do create bit wear.3

Once the wear patterns had been established, then archeological artifacts had to be examined and compared.  Dr. Anthony and his team was able to establish “that horses were bitted and ridden in northern Kazakhstan beginning about 3700-3500 BCE.”4

What impressed me is that the process of establishing their point was classic measurement, classic scientific method.  They started with a known fact: evidence of bit wear shows up in the teeth of horses.  After careful calibration of the pattern in modern horses, they explored a hypothesis, a concept that could lead to understanding: bit wear may show up in horses used by early steppe dwellers and if it can be established when wear patterns start to show up, perhaps this will also establish when people began to use horses for riding and pulling.  They then tested the hypothesis on actual horse teeth from the period in question, and have been able to establish an approximate time frame for when bit use began.

My concern, as always, is, does any of this help me figure out when and how people started to measure?  His focus is not on measurement – though there are artifacts that he discusses that most likely would not have existed without measurement: stone knives, jewelry, dwellings, wagons, chariots.  On this basis, the culture(s) that he describes were comfortable with measurement.

In his discussions of linguistic information, Dr. Anthony has provided some guidance in establishing that by the time of proto-Indo-European, measurement was a common activity.  His principal interest led him to discuss the reconstruction in proto-Indo-European such words as “wheel”, ‘axle’, “thill” (harness pole) and “ride” (convey or go in a wagon).

Evidently, since not all linguists agree with the reconstructions of proto-Indo-European words, either with the techniques or even with the possibility thereof, Dr. Anthony uses one of the easier, more transparent words as his example of the possibility of reconstructing proto-Indo-European words: “hundred”, the sounds of which he also ties to the sounds of the proto-Indo-European reconstruction of “ten”.  If the meaning of “hundred” is accurately attributed to proto-Indo-European, counting, and thus measurement, was well established by that time.

My conclusion is bolstered by the physical archeological evidence he discusses related to dwellings – some permanent dwellings where measured crossbeams for roofs would have been needed – and to both wagons and chariots.  A simple thought experiment makes this clear.  Imagine a chariot with two wheels of unequal size.  It would not roll straight without difficulty nor would the platform of the driver be level.  And if the wheels were not just different sizes but not very close to perfect circles, I can only imagine the warrior in the chariot ready to throw a spear or swing a sword and being jostled at exactly the wrong moment.  A wagon with four wheels would need additional measurement care to work well.

For some further corroboration of his description of the way of life of the steppe-dwelling proto-Indo-European speakers, Dr. Anthony cites the early written literature of two subsequent cultures, and the strong parallels between them in customs reflected in the literature: the Sanskrit Vedas which are sacred Hindu texts, particularly mentioning the Rig Veda, and the Avesta, in the Avestan language, sacred texts of Zoroastrians.

I had heard of both, but had neither read them nor done any research about them.  So, I took a bit of a detour, read the Wikipedia articles about both, then got copies of translations of both.  The Rig Veda version which I purchased in book form is one hundred and eight hymns from the Rig Veda, selected, translated and annotated by Wendy Doniger, Penguin Books, 1981,  is complete enough to give a flavor.  And since measurement words are used in the text as if they were common knowledge, no insight into the beginnings of measurement can be gleaned.  Some examples:

Hymn 2.12 titled ‘Who is Indra?’

Verse 2 – He who made fast the tottering earth, who made still the quaking mountains, who measured out and extended the expanse of the air, who propped up the sky – he, my people, is Indra.6   

Hymn 1.160 titled Sky and Earth

Verse 4 – Most artful of the gods, he gave birth to the two world-halves that are good for everyone.  He measured apart the two realms of space with his power of inspiration and fixed them in place with undecaying pillars.7

Hymn 2.28 titled Varuna

Verse 5 – Loosen me from sin as from a sash; let us find the fountainhead of your Order, Varuna.  Do not let the thread break while I am still weaving this thought nor let the measuring-stick of the workman shatter before its time.8 

One can only hope that the translations of the “measure” words is accurate and consistent, but since they are translations and my grasp of Sanskrit is non-existent, I have no way to confirm this without extensive research.

The Avesta that I obtained is a free version in Google Books, which was scanned from the Harvard University Library copy.  The translator is James Darmesteter, it was published by Oxford at the Clarendon Press in 1895, and while trying to read it on my iPhone, I developed a headache, since the text was so small.  Only after trying to work my way through the nearly 100 page introduction did I notice in the Wikipedia entry on the Avesta the citation under the Bibliography section: “A full translation by James Darmesteter and L.H. Mills forms part of the Sacred Books of the East series, but is now regarded as obsolete.”9

Elsewhere in the Wikipedia article, though, is the statement:

There are strong linguistic and cultural similarities between the texts of the Avesta and those of the Rigveda; the similarities are assumed to reflect the common beliefs of Proto-Indo-Iranian times, with the differences then assumed to reflect independent evolution that occurred after the pre-historical split of the two cultures.10

In the translations of both the Rig Veda and the Avesta, there are elements that do accord with Dr. Anthony’s thesis that the culture from which both evolved was deeply involved in horses, wagons, chariots, sacrifices, etc.  There was also an apparent understanding of celestial events beyond just sun- and moon-rise.  So, even though reading these two early works of literature was a digression bearing little fruit as far as helping to establish the beginnings of measurement, they were of value, since they showed evidence that humans had made progress in measuring aspects of their world.

Dr. Anthony’s work showed much about the way that professional archeologists work, how they date artifacts from the past, what methods they have for measuring and drawing conclusions about past cultures.  His is a wonderful book, if you like that sort of thing, and I do.

As I was working on this post, there was a bombshell dropped into the world of linguistics, which I would like to take up in the next post.

In the meantime, I did find a lovely quote about language and words in a book left in my bookshelf by my older daughter from her college days.  The book is called Chuang Tzu: Basic Writings, and contains translations of writings attributed to Chuang Tzu (or Zhuangzi).  Although he is evidently considered a philosopher of the Taoist school, a number of his paradoxical statements strike me as in the spirit of Zen, and the quote is one of those:

“The fish trap exists because of the fish; once you’ve gotten the fish, you can forget the trap.  The rabbit snare exists because of the rabbit; once you’ve gotten the rabbit, you can forget the snare.  Words exist because of meaning; once you’ve gotten the meaning, you can forget the words.  Where can I find a man who has forgotten the words so I can have a word with him?”11

---

1 http://www.nytimes.com/2008/03/02/books/review/Kenneally-t.html

2 Anthony, David W., The Horse The Wheel and Language, Princeton University Press, Princeton, N.J., 2007. pp 5-6.

3 Ibid. pp 208-209.

4 Ibid. p 220.

6 The Rig Veda, translated by Wendy Doniger, Penguin Classics, London, England, 1981. p. 160.

7 Ibid. p 203.

8 Ibid. pp. 217-218.

9 http://en.wikipedia.org/wiki/Avesta

10 http://en.wikipedia.org/wiki/Avesta

11 Chuang Tzu: Basic Writings, translated by Burton Watson, Columbia University Press, New York, N.Y., 1964.  p. 140.

Hours and Hours

I found myself wondering how time during the day was broken up into hours.  Noting the cycle of light and dark during days is pretty simple: every culture and every language as far back as I’ve been able to find has had the concept of daylight time and darkness time.  But how did the current scheme of 24 hours in a day, each hour with 60 minutes and each minute with 60 seconds, develop?  A second question that follows from this is, were other schemes considered, if so what were they, and why were they discarded?

Herodotus (c.490 BC to c 425-20 BC), in The Histories, Book 2, 109, adds an aside in his discussion of how Egypt developed geometry:

I think this was the way in which geometry was invented, and passed afterwards into Greece – for knowledge of the sundial and the gnomon and the twelve divisions of the day came into Greece from Babylon.1

Earlier in The Histories, Herodotus credits the Egyptians with the year (as quoted in the earlier post, Marking Time (or at least calibrating it)):

As to human matters, they all agreed in saying that the Egyptians by their study of astronomy discovered the year and were the first to divide it into twelve parts…the Egyptians make the year consist of twelve months of thirty days each and every year intercalate five additional days, and so complete the regular circle of the seasons.2

Egyptians and Babylonians, two of the earliest city civilizations, then, are responsible for some of the earliest time measurements, at least according to Herodotus.  They may be responsible for the earliest standardized time measurement, but I suspect that others before the formation of city civilizations could have started the process, and my guess is that the process had progressed sufficiently that some of the standardized concepts were not original with the Babylonians and Egyptians.

Pliny the Elder (23 AD to August 25, 79 AD3), in Natural History, has a slightly different take. In Book 2, Chapter 78, he states that the first sundial was made by Anaximenes the Milesian and was exhibited for the first time in Lacedaemon.  However, it is not clear in this first mention whether Anaximenes’s sundial was set up to measure hours, but later in Natural History, in Book VII, Chapter 60, Pliny states:

CHAP. 60 – WHEN THE FIRST TIME-PIECES WERE MADE.

…[I] have already stated, in the Second Book, when and by whom this art was first invented in Greece; the same was also introduced at Rome, but at a later period. In the Twelve Tables [the foundation of Ancient Roman law], the rising and setting of the sun are the only things that are mentioned relative to time. Some years afterwards, the hour of midday was added, the summoner of the consuls proclaiming it aloud, as soon as, from the senate-house, he caught sight of the sun between the Rostra and the Græcostasis; he also proclaimed the last hour, when the sun had gone down from the Mænian column to the prison. This, however, could only be done in clear weather, but it was continued until the first Punic war. The first sun-dial is said to have been erected among the Romans twelve years before the war with Pyrrhus, by L. Papirius Cursor, at the temple of Quirinus,…

M. Varro says that the first sun-dial, erected for the use of the public, was fixed upon a column near the Rostra, in the time of the first Punic war, by the consul M. Valerius Messala, and that it was brought from the capture of Catina, in Sicily: this being thirty years after the date assigned to the dial of Papirius, and the year of Rome 491. The lines in this dial did not exactly agree with the hours; it served, however, as the regulator of the Roman time ninety-nine years, until Q. Marcius Philippus, who was censor with L. Paulus, placed one near it, which was more carefully arranged: an act which was most gratefully acknowledged, as one of the very best of his censorship. The hours, however, still remained a matter of uncertainty, whenever the weather happened to be cloudy, until the ensuing lustrum; at which time Scipio Nasica, the colleague of Lænas, by means of a clepsydra, was the first to divide the hours of the day and the night into equal parts: and this time-piece he placed under cover and dedicated, in the year of Rome 595; for so long a period had the Romans remained without any exact division of the day.4

It appears, then, from Pliny, that the concept of “hour” was part of the Roman way of thinking.  There is a clepsydra mentioned for measuring the hours of the day and  night into equal parts.  “Clepsydra” is the name given to “water clocks”, which are usually bowls or basins with drains that are periodically filled or re-filled with water, and that drain at a predetermined rate.  The amount of water remaining was representative of the time.  But it looks as if, from Pliny’s article, that the hours of the day were divided into equal parts, and those of the night as well, but relying on the length of the day light by the season.

There is mention of a sundial in the Bible, in II Kings, Ch. 20, verses 9 – 11.  Isaiah refers to it to prove that the Lord is as good as his word to Hezekiah, by having the Lord make the shadow thrown by the gnomon move backwards by 10 degrees.  Hezekiah then believes.  I do not know the dates or chronology of the prophets or of the writing of the Bible well enough to say whether this occurred before Anaximenes or later, or if this is an artifact of translation: I have a King James version, which was translated in the early 1600’s.

In a very thorough book, History of the Hour, by Professor Gerhard Dohrn-van Rossum, the hour is described as basically having two separate conceptions from fairly early on.  He states that by the time of Christ’s birth, there was a division of the 24 hours into equal hours, but it was largely used by astrologers for horoscopes.  Otherwise, the Babylonians had divided the day into hours which varied: day time and night time were divided into 12 hours each, which meant that during the summer in Babylon and further north on the globe, the daylight hours were longer and in the winter, they were shorter.  The inverse happened to the night time hours: when daylight hours were longer in the summer, the hours of nighttime darkness were shorter and during winter nights, the hours were longer:

These hours were called temporal hours, “horae inequales.”  Expressed in minutes – which were unknown at the time – the ratio of the longest to the shortest daylight hour in Upper Egypt was 67:53, in Athens 73:47, in Rome 76:44, in southern Germany 80:40, in northern England 90:30.5

To work with these ratios, which represent the ratio of minutes of daylight at the summer solstice to the minutes of daylight at the winter solstice, by multiplying and finding map locations we get the following table.  At the times of the equinoxes, when the daylight time and nighttime darkness hours are equal, there are 720 minutes of daylight and 720 of darkness:

City	approx. Latitude	Summer Daylight	Winter Daylight
Alexandria	30o	804 minutes	636 minutes
Athens	38o	876 minutes	564 minutes
Rome	42o	912 minutes	528 minutes
Munich	47o	960 minutes	480 minutes
Newcastle	55o	1080 minutes	360 minutes

So, the further north one goes, the longer the daylight hours in summer and the shorter in winter, until one reaches the Arctic Circle, which is the line above which there are days in the summer when the sun does not set at all, and there is a time in the winter when the sun never rises above the horizon: darkness for several months.

In Newcastle in winter, one would have 6 of the equal hours to accomplish a day’s worth of tasks, essentially 12 segments 30 minutes long in the terms of the temporal hours.

There was a third division of the time during the middle ages for Christians, which is discussed in a number of places, including the book by Professor Dohrn-van Rossum.  These were defined times at which to perform the daily round of devotional prayers.  These were the hours that were used by monasteries for determining when the monks were to gather to pray.  At some point, the procedure changed from having one of the monks being designated the timekeeper, whose job it was to awaken the monks in the night and to call the monks during the day, to giving the job over to bells that were rung.  In the 13^th century, the earliest attempts were made to have a mechanical device ring the hours.  Professor Dohrn-van Rossum states “…that the combination of bell striking mechanisms with large water clocks is known around 1250…”6

By 1250, Chinese astronomers had created water-driven globes and armillary spheres.  These used water to power the mechanics rather that operating like the clepsydra.   The earliest mechanical clock, according to Joseph Needham, was completed in 725 AD, and was an astronomical instrument powered by water which also served as a clock.  The purpose of the astronomical instrument/clock was to time accurately the hours of conceptions of the Emperor’s children, that is, sons, so that the court astrologers could determine which of the sons had the most auspicious horoscope and should become the next emperor.

A successor instrument was built by Chang Ssu-Hsun in 976 AD, using mercury instead of water to power it, because mercury would not freeze in the middle of a cold night.  The most notable astronomical instrument/clock was built in 1092 by Su Sung.  It is notable in that it did use water again for power, and although it was destroyed by a following dynasty, because of extensive plans and drawings that have survived, a replica has been built which resides at the Science Museum in London.  It is possible that the rumors of these mechanical clocks with a form of escapement reached Europe, but the links are not certain and are tenuous at best.7

However, the work on establishing hours continued in Europe: King Alfonse X of Spain commissioned the Alfonsine Tables, based on a translation of Ptolemy’s tables, which then were used from the time they were completed during his reign from 1252 to 1284 AD.  Copies were made and circulated among the intelligentsia, and the Tables were first printed in 1483.  They were the standard tables for astronomers until the Rudolphine tables, based on the work of Tycho Brahe and finished by Johannes Kepler, were published in 1627.  In the Alfonsine tables,

…hours were divided into minutes, seconds and “terciae”, …[d]espite the ambiguous terminology, the rapid and broad diffusion of the tables must have promoted knowledge of the hour-minutes and hour-seconds in learned circles8

There is a passage in the Roman de la Rose, composed between 1275 and 1280, which alludes to something resembling mechanical clocks, but does not appear to be as clear as one might wish.  However by 1315 to 1320, there are two references to “clocks” in Dante’s Divine Comedy that could only be written if the author knew a little bit about clocks.

Then as a clock tower calls us from above
when the Bride of God rises to sing her matins
to the Sweet Spouse, that she may earn his love,

with one part pulling and another thrusting,
tin-tin, so glad a chime the faithful soul
swells with the joy of love almost to bursting-

just so, I saw the wheel of glories start
and chime from voice to voice in harmonies
so sweetly joined…

Paradiso, Canto X, ll. 138-147

So spoke Beatrice, and those blissful souls,
flaming as bright as comets, formed themselves
into a sphere revolving on fixed poles.

As the wheels within a clockwork synchronize
so that the innermost, when looked at closely
seems to be standing, while the outermost flies;

just so those rings of dancers whirled to show
and let me understand their state of bliss,
all joining in the round, some fast, some slow.

Paradiso, Canto XXV, ll 10-18 9

I have included a list of the third division of time, the devotional hours, which comes from the commentary included in a facsimile edition of The Hours of Jeanne D’Evereux, Queen of France, published by The Metropolitan Museum of Art, in New York.  The commentary was done by James J. Rorimer, Director of the museum, though the date of his notes is not given.  The facsimile was published originally in 1957, reprinted several times, with the last date given as 1973.

Hour name	Occurs
Matins	Midnight
Lauds	Sunrise
Prime	6:00 a.m.
Terce	9:00 a.m.
Sext	Noon
None	3:00 p.m.
Vespers	Sunset
Compline	9:00 p.m.

In the commentary, Rorimer dates the creation of the book to no earlier than 1325, when Jeanne and King Charles IV of France were married, and no later than 1328, when King Charles died, since the book was a gift from him to her.  If the commentary is correct, the devotional hours were measured by clock hours, by equal hours, in the early 14^th century.  There appears, from the Dohrn-van Rossum book, to be some question about when the actual adoption of equal clock hours occurred, but was no earlier than the late 13^th century, when the first mechanical “clocks” were set up built, originally to ring bells.

Clocks did not get faces until later in the 14^th century.  I am including pictures of the clock at Salisbury Cathedral, originally installed in 1386.

The clock with its descriptive sign first appeared in the post, A Slight Digression.

Outside of Salisbury Cathedral is another form of clock: a sundial, evidently set up in about 1749.  The sundial does indicate the hours: the picture was taken on a sunny day at about 5:00 in the afternoon.  The gnomon is not solid: it has one end of the pointer at the apex of the hour lines, and a support that is curved sitting just above half-way near the noon line.  The shadow of the indicator is just about at five (V).

The sign accompanying the sundial discusses another of the peculiar ways that time was measured: the Julian Calendar had shifted the seasons far enough out of synch that a major correction had to be made, which was done in England in 1752, and at other times in other parts of Europe.10

During the 14^th century, one of the questions was when to start the day.  We are familiar with the start of the day at midnight – 12:00 AM, 0:00 (zero o’clock on a 24 hour clock, or 24:00).  But some started the day at sunrise, and others started at sundown.  Some used a 24 hour clock, and some divided the day into 2 – 12 hour segments.  Among the Jewish and the Islamic religions, sundown is the start of various holidays.  Those that started at sundown designated any events that happened at night as happening during the succeeding day, while those which started at sunrise included the night’s events of the night following the day.  Until the “standard” was accepted to start the day at midnight, only Roman jurists, and those using the devotional scheme with the start of the day at Matins, used midnight at the dateline.   I have not found an exact date or event, but this became customary during the later 14^th century.

Along with when to start the day was the question of how to design the faces of the clocks.  Some went with a 24 hour face, most with a 12 hour face.  St. Mark’s Cathedral in Venice chose to use a 24 hour face, but put I and XXIIII in the place where we are accustomed to seeing 3:00.

The first clock housed in the tower was built and installed by Gian Paulo and Gian Carlo Rainieri, father and son, between 1496 and 1499, and was one of a number of large public astronomical clocks erected throughout Europe during the 14th and 15th centuries. The clock has had an eventful horological history, and been the subject of many restorations, some controversial.

After restorations in 1551 by Giuseppe Mazzoleni, and in 1615, by Giovanni Battista Santi, the clock mechanism was almost completely replaced in the 1750s, by Bartolomeo Ferracina. In 1858 the clock was restored by Luigi De Lucia. In 1996, a major restoration, undertaken by Giuseppe Brusa and Alberto Gorla, was the subject of controversy, amid claims of unsympathetic restoration and poor workmanship.11

In the earlier post, Surveying and Mapping, I mentioned a timekeeping scheme developed during the French Revolution, with 10 hours per day, 100 minutes per hour and 100 seconds per minute: it never gained many adherents and was dropped when Napoleon reached his accord with the Church.

With the advent of the mechanical clock and the ability to measure hours equally rather than using the temporal hours based on sunrise and sunset, the pace of mechanical invention quickened as the regulating by the clock of work, tasks, and daily events proliferated and permeated all of Europe and ultimately the rest of the world.  The mechanical clocks led to the prevalence of the clockwork universe model.  Hours were divided into minutes and seconds, and the tools to measure those further divisions were developed.  The tools are now so sophisticated that the term “nanosecond”, one billionth of a second, is a commonplace term.  I still have trouble, though, imagining the experience of a tenth of a second.

---

1 Herodotus, The Histories, Penguin Books, London, England.  Translated by Aubrey de Selincourt, 1954. Revised edition, 1972.  Revised edition with new introductory matter and notes by John Marincola 1996, further revision 2003. P. 136.  I had found so many “measurement” references to Herodotus that I bought a copy and am reading it.  Since Herodotus died around 425 and 420 BC, the book is surprisingly lively for 2400 years old.

2 Herodotus, The Histories, Penguin Books, London, England.  Translated by Aubrey de Selincourt, 1954. Revised edition, 1972.  Revised edition with new introductory matter and notes by John Marincola 1996, further revision 2003. P. 96.

3 The date of Pliny the Elder’s death is quite precise: he was killed trying to rescue a friend and his family during the eruption of Vesuvius.

4 Pliny the Elder, Natural History, Book VII, Chapter 60, Second English translation by John Bostock and H.T.Riley, 1855; complete, including index, found at:

http://www.perseus.tufts.edu/hopper/text?doc=Plin.+Nat.+toc&redirect=true

5 Dohrn-van Rossum, Gerhard, History of the Hour, Clocks and Modern Temporal Orders, translated by Thomas Dunlap, University of Chicago Press, Chicago, Ill, 1996. P.19.

6 Dohrn-van Rossum, Gerhard, History of the Hour, Clocks and Modern Temporal Orders, translated by Thomas Dunlap, University of Chicago Press, Chicago, Ill, 1996. P. 71.

7 Information about the Chinese astronomical instruments comes from Temple, Robert, The Genius of China, 3,000 Years of Science, Discovery & Invention, Inner Traditions, Rochester, VT., 1986,1998,2007.  The introduction was written by Dr. Joseph Needham, and the material was drawn from Needham’s epic multi-volume work, Science and Civilization in China.

8 Dohrn-van Rossum, Gerhard, History of the Hour, Clocks and Modern Temporal Orders, translated by Thomas Dunlap, University of Chicago Press, Chicago, Ill, 1996. P. 81

9 Dante Alighieri, The Divine Comedy, Rendered into English Verse by John Ciardi, W.W.Norton & Company New York, N.Y 191, 1965, 1967, 1970, 1977.

10 Big thanks for the Salisbury clock and sundial photos to my daughter, Branwyn Darlington.

11 http://en.wikipedia.org/wiki/St_Mark%27s_Clock

Both the picture and the quote are from the Wikipedia entry for St. Mark’s Clock.

Uncertain Results

In this post, we’ll follow on to one of the ideas from the last post: that statistics and statistical analysis are important tools for coping with measurements, especially when measurements accumulate in sufficiently large amounts with varying values.  When that is the case, the measurements are considered “raw data”.  Having at least a conceptual understanding of the way that statistical analysis is used to reduce volumes of data to comprehensible information must be considered a critical skill in dealing with our modern world.

My intention is not to teach statistics or statistical analysis: I used these tools a little in my professional life, but my use was limited, fortunately.  I have read several books on statistics as well as listened to Dr. Michael Starbird’s two DVD lecture series.  I have listed them at the end of this post so that you may read them, consult them or ignore them.  I am hardly an expert, but I do appreciate being able to understand what is meant when I hear statistics being used or misused, and I know enough to ask reasonable questions about hypotheses, data, sampling and drawing conclusions.  Does this mean that I am equipped to cope well with our modern world?  Maybe so, maybe no.  There’s no fool like the one convinced that he/she cannot be fooled.

In the 12th lecture in Meaning from Data, Dr. Starbird comments: “Statistics is all about coming to conclusions that are not certain.”  There is much about life that is uncertain, which is, of course, a truism but is not trivial.  Statistics are used to assess future risk.  Assessing risk, either for insurance purposes or building a nuclear power plant, is always an uncertain prospect, and when it is inadequately done, as has been made horribly clear in the case of the massive Japanese earthquake and tsunami, the consequences are potentially lethal.  Not only is the future uncertain but the past is too: what happened in the past is the subject of endless books and articles on history, archeology, paleontology, etc., not all of which agree.  Describing what happened in crimes is uncertain: memories of witnesses, if there are any, are often vague, and a large portion of the justice system would be rendered unnecessary if the past could be easily reconstructed (and our prisons even more over-filled?).  The kind of certainty that Sherlock Holmes provides is exactly what you would expect of a work of fiction, nice, but illusory.

Since uncertainty is a given in the human condition, is it the environment to which humans have adapted by using measurement to find certainty?  It does seem as if the driving force behind much of physical science from the 16th century until the beginning of the 20th century was to finally establish the certainty of the clockwork universe implicit in the work of Isaac Newton that is a gift Newton attributed to the ‘Creator’.

This clockwork universe started falling apart even before the work of Charles Darwin.  The dissolution received a push by The Origin of Species, since it began to look less and less likely that evolution was under the direct control of a creator, or at least, that evolution could have occurred in ways that required a creator.  But the apparent collapse of the clockwork universe was completed by Einstein’s relativity theories, the special and the general, then with the work of the group associated with Niels Bohr.  I say apparent since both relativity and quantum mechanics have carefully defined realms where they are effective models of behavior: relativity, when dealing with velocities that approach the speed of light; and quantum mechanics, the realm of atomic and sub-atomic matter.  Newtonian mechanics explains most of what we experience in the macroscopic world pretty well, and is still used for the calculations guiding most space shots, though relativity figures in to the way that the Global Positioning System works – but more on GPS in a later post.

Since statistics has been on my mind, I realize that the way that I think about the realms of quantum mechanics, relativity and Newtonian mechanics can be represented as a picture: using a standard bell curve, the normal distribution curve from statistical analysis, with two lines marking the extreme ends, the green is where quantum mechanics operates, the red represents the Newtonian world that is most of our day-to-day experience, and the yellow is the realm of relativity.  The following picture is a picture only and was generated without reference to any actual data.  Therefore, the green and yellow areas might have to be smaller, the red might need to be broader, but this representation was done to clarify a concept, and not to provide actual representations of the realms.  Pretty, but like any model, it has lots of inaccuracies: the foundation for the red can be found in both the green and the yellow.

One concept that is part of the Copenhagen interpretation of quantum mechanics is Heisenberg’s famous uncertainty principle.  The uncertainty principle has a very precise meaning in physics: that if you try to measure the precise position of an electron, one of the sub-atomic particles, you will not be able to measure its momentum, and the inverse, if you try to measure its momentum, you will be unable to measure its position.  The two quantities, position and momentum, cannot be measured simultaneously.  Because the only way to measure them is to use electromagnetic photons (like light but including the full spectrum of electromagnetic radiation) and the energy of small wavelength photons is comparable to the energy of an electron, “The more an observer trie[s] to extract information about the electron’s position, the less it [is] possible to know about its momentum, and vice versa.”1

This represents the limit of measurement: anything that is the size of wavelenths2, whether light wavelengths or x-ray or gamma ray wavelengths, the last two being the shortest, can’t be measured with precision.  To be observed using electromagnetic photons, one must “bounce” the photons off the object, and then view the photons.  If one tries to bounce a photon off an electron, sometimes it will be absorbed, sometimes it will knock the electron out of orbit, sometimes it might be reflected.  But anything that can reflect the photon without being substantially affected by the interaction can be measured.  In terms of the dimensions that this deals with, the change in momentum multiplied by the change in the position of the electron is equal to one/half of the reduced Planck constant, the value of which is 1.0545 x 10 to the minus 34^th power joules per second.  Things just don’t get much smaller.

To use a particle analogy, if one tries to bounce a billiard ball off a ball bearing, the interaction will send the ball bearing flying, changing its position, changing its momentum.  The result would be that maybe some billiard balls would come back, as if they had bounced off the cushion of a billiard table.  Others would keep going, having sent the ball bearing flying, and some might just graze the ball bearing.  The resulting “picture” of the ball bearing would be “fuzzy” at best.

In the book quoted above, Lindley says that Heisenberg originally used the German word for “inexactness”, but Bohr came up with the word “uncertainty”.  Lindley provides more information on the use and misuse of words about this aspect of quantum mechanics, but it is the phrase “uncertainty principle” that concerns me.

The phrase has been taken as a metaphor and applied to all sorts of situations in the macroscopic world that are only marginally, if at all, applicable.  A corollary of this is that the observer affects that which is observed – possibly true in the situation of an anthropologist observing a group of people, who may or may not put on a “performance” for him/her, but not necessarily true of an archeologist finding human or animal bones in a prehistoric grave.  There are some effects an archeologist could have, of course, accidentally running their shovel through a bone, shattering it, or moving a bone so that the precise location is no longer reconstructable, and if the bone was to be Carbon 14 tested, contaminating it by touching it with his/her bare hand.

The warning here that I want to issue is to be very wary of those who take a carefully worked out bit of a scientific model and apply it as a metaphor to a completely different realm.  Another case in point is the theory of genes and evolution being turned into a model for the evolution of ideas, the meme theory.  It may be helpful for a time, but could be misleading in the long run.

Trying to describe life based on the uncertainty principle has the same caution, even though it may seem “poetically accurate”.  Yes, quantum mechanics uses probability in its model of the way that the sub-atomic world interacts, and yes, many macroscopic, human events use probability to deal with the future, with risk, and even in reconstructions of the past, but the two realms, sub-atomic and macroscopic operate differently, and logic and reasoning techniques that work in one realm do not always make the leap across the gap successfully to the other realm.

In all probability, this gap is bridged successfully only 5% of the time.  That statistic, by the way, comes under the heading of what my older daughter told me: 43% of all statistics are made up on the spot.  (or was it 48%?)  She may have been paraphrasing an old Peanuts cartoon.

While I make light of statistics, and I could probably provide you with more statistics being blatantly and humorously misapplied, there is some serious intent here.

The 11 February 2011 issue of Science magazine, the journal of the American Association for the Advancement of Science (AAAS) has a special section in it devoted to data.  There are 3 articles under the category “News”, 11 articles under the category “Perspectives”, and a series of related informational articles about the challenges of dealing with the data overload that has been created.  One article which is only online and requires either membership or payment for a copy of it, is one that concludes that “We have recently passed the point where more data is being collected than we can physically store”3 If you would like to look at the articles, there is public access to those in the two categories that I mentioned above at:

http://www.sciencemag.org/site/special/data/

The first story in the News category describes what happens to data after the physicists move on to the next big collaboration – the data may be “misplaced”.  The tale is of a physicist going back to review the data from an experiment he had worked on 20 years before, and discovering that the data had been scattered, the software to access the data was obsolete, and “,,,[o]ne critical set of calibration numbers survived only as ASCII text printed on green printer paper…”4 which took a month to reenter by hand.  Eventually, several years were spent reconstructing the data, then using it in light of the most recent theoretical advances to provide material for a number of papers, including one of which was cited in a Nobel Prize.  But this recovery effort was part of the inspiration for the formation of a working group at CERN called Data Preservation in High Energy Physics (DPHEP).

The second story in the News category describes two collaborations on visualization software, both of which are cross-disciplinary: both collaborations are medical people and astronomers.  One collaboration involves medical software used in MRIs to display 3-D versions of the MRI results, and has been adapted to the display of a massive amount of astronomical data in 3-D, leading to “…new discoveries that are incredibly difficult to do otherwise, such as spotting elusive jets of gas ejected from newborn stars.”5 The other collaboration uses image-analysis software developed for astronomers to “…analyze large batches of images, picking out faint, fuzzy objects”6, adapted to automate cancer detection.  It is a very exciting use of software that uses statistical techniques to deal with masses of data.

I have included mention of these stories because they indicate how serious the ability to deal with data is using statistical analysis – and ultimately how important understanding how to transform data into information is.  Since the central theme of the posts is measurement, statistics are critical to understanding many kinds of measurement, from economics to physics, from sports to carpentry, etc.  I hope that I have convinced you of the value of understanding how statistics are generated from various kinds of data sets.

A little “bookkeeping” relative to the posts as a whole.  In two earlier posts, Marking Time (or at least calibrating it) and Measuring Light, I mentioned Ole Roemer’s brilliant attempt to measure the speed of light by observing the moon of Jupiter named Io when it disappeared behind Jupiter and then reappeared.  I recently received a photo from the Hubble Telescope through an iPhone app, Star Walk, that shows Io as it transits in front of Jupiter.  It’s such a great photo that I’ve included it below:

The tiny dot in the center is Io, the dot to the right and down a bit is Io’s shadow on the surface of Jupiter, and of course, the background is Jupiter.

The other piece of bookkeeping is that in the post titled Science and Measurement, I discussed the work of Thomas Kuhn, in particular, his book The Structure of Scientific Revolutions, and an article that he wrote called The Function of Measurement in Modern Physical Science.  I treated him as an authority on how science measures and moves forward from paradigm shift to paradigm shift.  This past week, a blogger? guest columnist? smart guy who has written several very interesting series of articles for the New York Times, Errol Morris, wrote a series of 5 articles with the overall title “The Ashtray”.  While not strictly about measurement, I learned much from the articles.

Errol Morris is, among other things, a film maker who won an Oscar for the best documentary in 2004 for his film, The Fog of War: Eleven Lessons From the Life of Robert S. McNamara. This set of articles, “The Ashtray” caught my attention when I read in the first one that Morris had been a student of Thomas Kuhn’s at Princeton, and that in 1972, Kuhn had settled a debate with Morris by hurling an ashtray at him.  The series goes on to discuss how Kuhn may not be the authority on scientific measurement that I thought he was.  I enjoyed the five articles quite a bit, so here are the URLs for them:

http://opinionator.blogs.nytimes.com/2011/03/06/the-ashtray-the-ultimatum-part-1/

http://opinionator.blogs.nytimes.com/2011/03/07/the-ashtray-shifting-paradigms-part-2/

http://opinionator.blogs.nytimes.com/2011/03/08/the-ashtray-hippasus-of-metapontum-part-3/

http://opinionator.blogs.nytimes.com/2011/03/09/the-ashtray-the-author-of-the-quixote-part-4/

http://opinionator.blogs.nytimes.com/2011/03/10/the-ashtray-this-contest-of-interpretation-part-5/?scp=4&sq=Errol%20Morris&st=cse

I guess that unless one spends much time in the actual field in which a person has won their fame or notoriety, one does not know how much uncertainty there is about that person’s reputation.

With that last bit, I will end this post which seems to have drifted from its original promise or premise, but contains a number of ideas that I believe is closely related to the subject of measurement.

________________________

A bibliography of a sort for the information in the post:

Hughes, Ifan G. & Hase, Thomas P.A., Measurements and their Uncertainties, A Practical Guide to Modern Error Analysis, Oxford University Press, Oxford, England, 2010.

Lindley, David, UNCERTAINTY: Einstein, Heisenburg, Bohr, and the Struggle for the Soul of Science, Doubleday, New York, N.Y., 2007.

Kachigan, Sam Kash, Multivariate Statistical Analysis, A Conceptual Introduction, Second Edition, Radius Press, New York, N.Y., 1991

Sanders, Donald H., and Smidt, Robert K., Statistics: A First Course, Sixth Edition, McGraw-Hill, Boston, etc. 2000, 1995.

Starbird, Professor Michael, Meaning from Data: Statistics Made Clear, The Great Courses, Chantilly, VA, Course No. 1487, 2006. www.thegreatcourses.com

Starbird, Professor Michael, What are the Chances?: Probability Made Clear, The Great Courses, Chantilly, VA, Course No. 1474, 2006. www.thegreatcourses.com

---

1 Lindley, David, UNCERTAINTY: Einstein, Heisenburg, Bohr, and the Struggle for the Soul of Science, Doubleday, New York, N.Y., 2007. pp. 146-147.

2 See the post titled Measuring Light for a description of the sizes of light wavelengths.

3 ” Dealing with Data, Challenges and Opportunities: Introduction”, Special Section, SCIENCE, AAAS, Washington, D.C., Vol 331, 11 February 2011, p. 692.

4 Curry, Andrew, ” Dealing with Data, Rescue of Old Data Offers Lesson for Particle Physicists”, Special Section, SCIENCE, AAAS, Washington, D.C., Vol 331, 11 February 2011, p. 694.

5 Reed, Sarah, ” Dealing with Data, Is There an Astronomer in the House”, Special Section, SCIENCE, AAAS, Washington, D.C., Vol 331, 11 February 2011, p. 697.

6 Reed, Sarah, ” Dealing with Data, Is There an Astronomer in the House”, Special Section, SCIENCE, AAAS, Washington, D.C., Vol 331, 11 February 2011, p. 696.

Errors In Measuring

In a post in November, 2010, called “2 Geodetic Surveys”, I described a geodetic survey done in Peru in the 18^th century by a group of French scientists.  One technique that was used, and variations of it are always used in well done surveys, was to have two teams perform the same measurements and calculations and compare the results.  The French were trying to measure the length of a degree of arc near the equator, and, using a French length unit, the toise which is 6 Paris feet and 6.39 English feet, one team got a result for a degree of longitude of 56,749 toises and the other team’s result was 56,768 toises.  This is a difference of 19 toises, or approximately 0.0335%.  That’s about 121 (English) feet difference over about 68.73 miles, which is about 362,894 feet.1 Those results are in incredible agreement, especially if you factor in the difficulties that they had obtaining any results, let alone these results.

The basis of information for the other survey discussed in that same post is Ken Alder’s book, The Measure of All Things.  This other survey was the measure of longitude with which to establish the length of a meter, which was performed subsequent to the French Revolution by Pierre Mechain (1744-1804) and Jean-Baptiste-Joseph Delambre (1749-1822).  They too were successful, ultimately, but not without difficulty.  In “Chapter 11 – Mechain’s Mistake, Delambre’s Peace”, Alder describes a strange condition that had developed over the course of the survey.  Mechain, as described by Alder, was a meticulous astronomer, given to depression, doubt and obsessive attention to detail.  His own measurements did not agree exactly nor meet his exacting standards, though they are, in retrospect, some of the best that had been done to that date.  He ended up fudging results, changing figures to make himself look better, but in essence, trying to cover up “mistakes” that were, to him, intolerable.  When Delambre received Mechain’s raw data, after Mechain died of yellow fever while trying to correct the observations, the data was not in clear, bound notebooks but on scraps of paper with erasures, lack of dates, etc..  Delambre carried forward his colleague’s cover-up, cleaning it up so that it was presentable enough, because he found that the ultimate results of Mechain’s were “correct”, erring mostly in the size of variations among his observations.  All the erasures and corrections did not affect the result, but made Mechain’s work look as if it had been performed better than it actually was.  Various instrumental problems, such as wear and lack of calibration, have been blamed, but midway through the discussion, Alder makes a statement that opened up a whole different path for discussing measurement.

In the end, Mechain came to blame himself – to his eternal shame and torment. …There is, however, one other possibility.  What if nothing and no one was to blame?  Indeed, what if there was no meaningful discrepancy at all?  That is: what if the error lay neither in nature nor in Mechain’s manner of observation, but in the way he understood error?  Twenty-five years after Mechain’s death, a young astronomer named Jean-Nicolas Nicollet [1786-1843] showed how this might be the case…

Mechain and his contemporaries did not make a principled distinction between precision (the internal consistency of results) and accuracy (the degree to which those results approached the “right answer”).2

This raises several questions, and as usual with questions, some of the answers lead to even more questions.  Let’s start with “the way he understood error”.  What can that possibly mean?  I was taught, in math anyway, there is a right answer and there are wrong answers.  I have heard about degrees of wrong, as in “a little wrong”, or “flat-out wrong”, but I can’t remember degrees of right.

Actually, the definitions for precision and accuracy stated in the quote get us pointed in the right direction.  If we think about the first mentioned survey, where there was a difference of 19 toises between two results, this is a situation that occurs regularly in all measurement: the first time you measure something may not agree with the second or other subsequent measurements.  What is causing the problem?  Is it the temperature, it was warmer on day two than day one, so maybe the metal tape measure or ruler had “expanded” a little with the heat.  That would result in what was measured registering as a little smaller on day two.  Maybe the tape measure or ruler was sufficiently constant, but since you were measuring a piece of wood and it rained during the night, the damp caused it to swell.  Maybe on day one you did the measurement, and on day two you had your friend do it.  There can be individual human variations in the way that measurements are captured.  So how can anything be measured accurately and with precision?

The method that has been developed in the last 200 or so years is called statistical analysis, and includes techniques and mathematical concepts for dealing with multiple “measurements”, also known as data points.   (I can hear groans, and yes, I feel the same way about statistics – if ever there was a boring subject…).  If you are going to talk about measurement, though, statistics cannot be ignored.

One important concept in statistics is the mean of a data set: commonly known as an average.  For our Peruvian measurements, 56,749 and 56,768 toises, we add them together and divide by two: 56,758.5 toises.  But we can provide a little more information by indicating the range of the two measurements if we add ± 9.5 toises.  The “±” means plus or minus, so if you add 9.5 to 56,758.5, you get 56,768, and subtracting 9.5 from our average or mean gives 56,749.  So, a common way to express a result of measurements is 56,758.5±9.5 toises.

This would be impractical, say, for a cabinet maker who wants the edges of the drawers to line up correctly: cut a piece that is 14.5±0.25 inches.  The phrase drilled into apprentice cabinet makers, carpenters, etc., is “measure twice, cut once”.  But they must use a number that does not have the “±” because the average is not going to give them a clean finished product.  But “±” is useful for certain types of measurement.

I started the questions with Mechain’s understanding of error.  Being obsessively concerned with details and having built his reputation on the accuracy of his observations, when he found that the variation in his multiple observations was too high, evidently he thought this reflected on his ability to provide accurate observations.  What Nicollet noticed, however, was that over time, Mechain’s “errors” tended in a similar direction, so he suggested that there had been wear in Mechain’s instrument that made “level” actually be tilted in the same direction every time the instrument was set up, and got worse over the seven years of observing.

The trick was to compensate for any change in the instrument’s verticality by balancing the data for stars which passed north of the zenith (the highest point of the midnight sky) against those which passed south of it.  Because Mechain had measured so many extra stars, such an operation was possible.3

What Nicollet did, then, was to average the north-passing stars, then average the south-passing stars, and then average the two averages.  He discovered that the most egregious error, which looked as if there was a difference in the readings of nearly 400 feet was actually accurate to within 40 feet.

By the time Nicollet started working on Mechain’s data, some new techniques had been developed by several mathematicians, but since developing new techniques are rarely without controversy, these were too.  Adrien-Marie Legendre (1752-1833) developed a method called “…the least squares method, which has broad application in linear regression, signal processing, statistics and curve fitting.”4 In 1805, he published his discovery.  The Prince of Mathematicians, Carl Friedrich Gauss (1777-1855), noted for not publishing nearly as much as he should have, announced that he had been using the method since 1795, and pretty much proved his case, by having predicted a position for Ceres in 1801.

Ceres, a dwarf planet/asteroid in the asteroid belt between Mars and Jupiter, had been observed early in 1801 for a short time by Giuseppe Piazzi (1746-1826) and the observed positions were published in September 1801.  By then, Ceres had disappeared into the glare of the sun.  Gauss used the observations to calculate and then announce where it would re-appear and when.  He was correct to within half a degree, and Ceres was found again.  Among the calculations he used was the least squares method, a method that is used to match actual observations with a model developed from the actual observations, and assumes that the experimental or observational errors have normal distributions.  A “normal” distribution is one name for the famous “bell curve”, another name for it is a Gaussian distribution.

Regardless of who was first, this was among the techniques that have been used to apply statistical analysis to all sorts of problems.  Are statistics a form of measurement?  Well, not really, but….

In order to deal with the unavoidable variance of measurements in a number of fields, “errors” that appear to arise just from the process of measuring, a method had to be developed.  There were a number of contributors to the method, statistical analysis, but now the method has “hardened” into a set of standard mathematical definitions and procedures.  If one uses them correctly, others may dispute some parts of the questions being addressed, but not how the conclusions were reached.  A pretty bold statement for a field defined by “…lies, damned lies, and statistics.”  There are legitimate ways to dispute meanings drawn from an experiment, but as long as there are no mistakes in the math, the statistical procedures don’t suffer from being questionable.  If one starts from assumption A, proceeds to gather data about this assumption, develops a hypothesis, then works the statistical procedures on the data and announces the result, the questions are not about the statistical procedures but about the assumption, the data, the hypothesis and the inferences.  And the dispute can be to the application of the statistical procedures to the data, but not about the statistical procedures themselves.  It is possible to “lie” with statistics by miss-applying the procedures to a data set, but, as pointed out by Dr. Michael Starbird in a series of lectures I have been watching, it is easier to lie without statistics.

Dr. Starbird’s lecture series, called Meaning from Data: Statistics Made Clear, is available through The Great Courses, and can be ordered through:

www.thegreatcourses.com

I am enjoying the lectures: he is clearly knowledgeable and presents well.  Plus, he was recommended to me by one of my daughters, who was the development editor for a wonderful textbook that he and another professor, Edward B. Burger, wrote, called The Heart of Mathematics, An invitation to effective thinking.  I’ve read large portions of that text and enjoyed his and Dr. Burger’s way of presenting “complicated” mathematical concepts.

To put this back together, though, it is in the 6^th lecture in Meaning from Data that Dr. Starbird discusses the Bell Curve, also known as the normal curve or the Gaussian curve.  He attributes the first working out of the curve to the work Gauss did to locate Ceres.  Did Gauss measure where Ceres was?  No, that was done by the astronomer, Giuseppe Piazzi, who recorded 24 observations during January and February of 1801.  Gauss took the observations, and used the statistics to define the path and the rate of travel on the path, to build a “model” of how Ceres would behave.  Nothing proves the value of new mathematical models like successful predictions, and Gauss was just about dead on.

Subsequent to this, Nicollet used the same kinds of statistical methods to deal with the “errors’ in Mechain’s observations, and was able to prove that Mechain’s errors were not errors, but variations within the tolerable for a precise and accurate understanding of the material needed to establish the correct length of the meter.

To now answer the question, ‘is statistics measurement?” the full answer is no, but it is a set of mathematical definitions and procedures, concepts if you will, that allow building of models from measurements.

While I had wanted to put more into this post, this has been a difficult one to write, and probably to read: no pictures.  The other information will wait for the next post, when I will have to spend some time on the only other subject in math that invariably (or probably?) makes people nod off to sleep: probability.  I will close by repeating my favorite question about the limit of using the concept of averages, originally posed to me by a friend and workmate, Bruce Poole.

If you had your right foot in a bucket of boiling water, and your left foot in a bucket of ice water, on average, would you be comfortable?

To remedy the no-pictures problem, below are two bell curves: normal distributions: Gaussian distributions.  The first is just the curve5, the second6 shows 3 curves, one with a standard deviation of 1, a second with standard deviation of 2, and the third with a standard deviation of 3.  We will talk more about this in the next post as well.

---

1 Whitaker, Robert, The Map Maker’s Wife, Delta Trade Paperbacks, 2004, New York, N.Y. (toises are discussed on p.48, the degree results are on pp 166-167)

2 Alder, Ken, The Measure of All Things, Free Press, a division of Simon & Schuster, Inc., 2002 New York, NY pp 298-299.  I added Nicollet’s dates to the quote.

3 Alder, Ken, The Measure of All Things, Free Press, a division of Simon & Schuster, Inc., 2002 New York, NY p.300.

4 http://en.wikipedia.org/wiki/Adrien-Marie_Legendre

5 Kachigan, Sam Kash, Multivariate Statistical Analysis, A Conceptual Introduction, Second Edition, Radius Press, New York, N.Y., 1991. p.31.

6 Hughes, Ifan G. & Hase, Thomas P.A., Measurements and their Uncertainties, A Practical Guide to Modern Error Analysis, Oxford University Press, Oxford, England, 2010. p. 13.

Measuring Light

In my office window, I have a chunk of clear glass with a clock mounted in it, which, when the light in the afternoon hits it, projects amazing rainbows around the walls and floor of my office.

I thought you might enjoy seeing one of the rainbows: such wonderful colors.

As I am determined to understand measurement, I look at the rainbows and think of ways that light can be measured.  There are a few that come to mind, but this list is surely not definitive  – measuring reflections, measuring refractions, figuring out where the colors come from and then measuring the wavelengths of the colors, measuring the speed of light.  What is the history of performing these four types of measurement?

First, do these measurement techniques meet or match the elements of measurement, as listed to the right?  Certainly they do: as I have written about these measurements in this post and posted it, others can read it, so the social element has been met.  The next element, when measuring light, the intention is to capture some characteristic of its behavior for understanding so that it can be communicated, at least.  Is there sufficient language to do that, not just the words but the concepts behind the words?  This is a tricky question, since there have been competing concepts about the nature of light over the centuries, the most recent of which is Einstein’s brilliant but weird synthesis.  There are ways to capture whatever insights into the nature of light we want to look at, and some standards that have been developed that can be used to make sure we are discussing common measurements.

Of course, once knowledge is there, the onboard computer (a.k.a. brain) doesn’t have to do a review each time, since one can look at the colors and be dazzled by them, with or without understanding the concepts or what has been measured.  For me, though, I find that anything in nature that is as beautiful as the rainbows cast by the prism/clock is enriched by knowing as much as I can about the phenomenon, although I rarely have to review the scientific understanding while viewing or experiencing the phenomenon because the knowledge is already there.

Looking at the history of the measurement of light provides some remarkable information about the development of measurement as well as the development of the concepts to understand light.

It is impossible to guess how primitive humans understood light: the first Greek to describe light with any accuracy is Empedocles (c 482 – c 432 BC), who “..claim[ed] that light has a finite speed.”1 Aristotle (384 – 322 BC) disagreed: he felt that light did not move, though in reading several interpretations of what he did say about light, his view seems a bit muddled.  It was almost as if he was saying that light is part of what we exist in, much like fish exist in water.  A further view of light was that developed by Euclid (around 295 BC) and subscribed to by Ptolemy (about 100 – 170): the eye sends out rays to see with.  Based on Euclid’s model, Heron of Alexandria (10 – 70) reasoned that the speed of light has to be infinite, because when you open your eyes at night, you immediately see distant stars: no time elapses between opening and seeing.

This is where the understanding of how the eye works, what light is and what the speed of light is, stood for nearly 1000 years.  In 1021, a very smart Islamic scientist named Abu ‘Ali al-Hasan ibn al-Hasan ibn al-Haytham (c 965 – 1041), westernized as Alhazen, completed an influential book called Kitab al-Manazir, translated as Book of Optics.  He accurately described a number of the behaviors of light, and also claimed that light from objects was delivered to the eye, not rays from the eye to the object.  The book was translated into Latin in the late 12^th or early 13^th century, and was printed in 1572.  This work influenced Roger Bacon and Johannes Kepler, among others – though it is not clear if Isaac Newton knew of it or of its commentaries.

Some of the contents of his book include:

• Proof that light travels in straight lines.
• Accurate descriptions of light being reflected by reflective surfaces.
• Accurate descriptions of light being refracted by clear media other than air – stating that light travels more slowly through water and glass.
• A clear and accurate description of how camera obscuras work.
• The nearly correct presentation of the physiology of the eye – though he thought the pupil was the receptive organ of light, he hinted that the retina would be involved, and he also stated that the optic nerve delivers what the eye captures to the brain for the brain to turn it into vision.

Al-Haytham’s near contemporary, Abu Rayhan al-Biruni (973 – 1048), westernized as Alberonius, added one more piece to the puzzle: he discovered that light traveled faster than sound.  And some years later, Kamal al-Din Farisi (1267 – 1319) wrote a correction to al-Haytham’s Book of Optics, in which he corrects al-Haytham’s theory of color, and correctly describes rainbows.  He used a clear glass sphere filled with clear water inside a camera obscura, and introduced light into the camera obscura through the pinhole.  The result was the “decomposition” of white light into the various colors of the rainbow.  At nearly the same time as al-Farisi’s discovery of how the rainbow phenomenon works, Theodoric of Freiberg discovered the same thing: there is no evidence of contact between the two, so the discoveries were most likely independently made.

The foundation of the modern understanding of how light behaves, then, had been developed by the late 13^th, early 14^th century.  The baton of scientific endeavor was passed to Europe around then, and work on light continued.

Johannes Kepler (1571 – 1630) evidently believed that the speed of light was infinite, as did Rene Descartes (1596 – 1650).  Galileo Galilei (1564 – 1642) performed an experiment to see if there was a speed of light, in about 1638.  He used a method similar to that used to figure out the speed of sound, an experiment done in the years preceding his light experiment.  The speed of sound was determined by firing a cannon, and having an observer a mile or so away time the difference between seeing the flash from the muzzle of the cannon and the sound of the cannon.  Galileo had an assistant with a lantern go to a hill a mile or so away from him, he uncovered his lantern and the assistant uncovered his when he saw the light from Galileo’s.  Galileo timed how long it took from when he uncovered his to the time he saw the light from his assistant’s lantern.  He concluded that if light is not infinitely fast, it is very very fast, since the timed interval was the same as when his assistant was six feet away, so the interval depended on human reaction time, not the speed of light.  “Based on the modern value of the speed of light, the actual delay [attributable to the speed of light] in the experiment would be about 11 microseconds.”2

In order to time the speed of light, the timing mechanism had to be accurate and standardized.  In an earlier post, “Marking Time (or at least calibrating it)”, I mentioned the work of Christiaan Huygens (1629 – 1695), who developed the first pendulum clock in 1656, increasing the accuracy of clocks to within 15 seconds per day.  I also mentioned Ole Roemer (1644 – 1710) who in 1676 realized that the movement of one of Jupiter’s moons seemed to have some timing problems.  Rather than re-write what I said, I will quote:

…the transit of the moons of Jupiter had been precisely timed: when several of the moons went behind Jupiter and reappeared had been timed precisely enough that one astronomer, Ole Roemer in 1676, had proved that the speed of light was finite using the occultation of Io, one of Jupiter’s moons.  He timed the occultation when the earth in its orbit was nearer to Jupiter, then when earth was at a different part of its orbit, much further from Jupiter, and noted that the times of occultation took much longer when the earth was farther from Jupiter.  This he correctly assumed was because the distance was so much greater, and reasoned that because of that, light had a finite speed and was not infinitely fast.

Roemer did not calculate a speed for light, but based on the timings he published, Christiaan Huygens did a calculation that came up with a speed for light of about 220,000 kilometers per second (km/s), which is not quite enough: the modern measure is about 300,000 km/s.  It should also be pointed out, while mentioning Huygens, that he published work on optics in which he stated his belief that light was composed of waves.  But more on the speed of light a little later.

A contemporary of Roemer and Huygens, Isaac Newton (1642 – 1727)3, the English genius, studied and wrote about optics.  He is associated with prisms being used to decompose white light into its constituent colors, among other things, and for his stance on the nature of light.  By his time, light was showing behavior that was like that of particles as well as of waves.  He used the measurements of reflection to “prove” that light consists of particles.

A light is reflected at the same angle to the perpendicular (the “normal”) of a flat mirror (a plane) as the angle of the incoming light ray to the perpendicular.  In math-ese, the angle of incidence to the normal is the same as the angle of the reflectance to the normal, very much like a billiard ball being shot at a cushion on a billiard table.  And even though light also showed wave-like behaviors, Newton felt the wave-like behaviors were not significant.  Because of his great prestige, scientists only looked for and used particle-like behavior in their experiments.  Until about 1801.

In 1801 or thereabouts, the results of the double-slit experiment, attributed to Thomas Young (1773 – 1829), became known.  Shining a light through a card with two slits near to each other and letting the light project onto a screen beyond the card shows a pattern of light and dark which is best explained by the interference of waves.  This “proved” that light was waves, not particles, and so the description remained until Albert Einstein redefined the nature of light.  But for much of the 19^th century, many of the measurements of light were devoted to its wave nature, with Newton’s particle theory being eclipsed.

One concept related to waves is that they require a medium in which to travel, much like waves in water, or sound waves in air.  As an example of an inaccurate analogy applied incorrectly, this led to a hypothesis that space, whether between the celestial bodies or here on Earth, was filled with a medium that transmits light waves, called “ether” or, as it was called in the 19^th century, “luminiferous ether”, meaning “light-carrying ether”.  We’ll get to an experiment that was done to figure out the effect of the ether in a little bit, but first, another consequence of the double-slit experiment: the measurement of wavelengths – the measurement of color.

“Furthermore, from the spacing of the interference bands of light and dark, Young could calculate the wavelength of light.”4 The figure he came up with was on the order of a fifty-thousandth of an inch.  This figure was improved upon by Anders Jonas Angstrom (1814 – 1874) who not only measured the wavelengths of the various colors, but developed a unit scale for the size.  The unit is equal to one-tenth of a millimicron (1 millimicron = a ten-millionth of a centimeter), and was subsequently named after him: an Angstrom.  So, although there are no sharp divisions between the colors, the ranges for colors are:

Red = 7600-6300 angstroms

Orange = 6300-5900 angstroms

Yellow = 5900-5600 angstroms

Green = 5600-4900 angstroms

Blue = 4900-4500 angstroms

Violet = 4500-3800 angstroms5

A further consequence of this work with spectrums was the development of spectroscopy.  Without going into spectroscopy too deeply, during the 19^th century, Joseph von Fraunhofer (1766 – 1826) discovered black lines in the spectrum from the Sun and from other heavenly bodies.  He measured them meticulously, but his work was ignored until Gustav Robert Kirchhoff (1824 – 1887) working with a collaborator, Robert Wilhelm Bunsen (1811 – 1899) (he of the famed burner…) explored the emission colors of various elements.   Kirchoff and Bunsen found that each element had a characteristic pattern of wavelengths/colors which could be used to define them, which were produced when they were heated to incandescence.  He also figured out that when he used a carbon arc to produce white light, and ran the light through the vapor of a heated element, the dark lines seen and measured by Fraunhofer matched the wavelengths of the characteristic element signature in emitted light.  As a result, it was realized that one could figure out the elements in stars and other heavenly bodies by spreading the spectrum the way that Fraunhofer had done, and checking the wavelengths at which the dark lines, the absorption lines, appeared.  A whole new way of measuring the stars was born.  One of its great successes was the discovery of helium in the sun’s absorption lines well before helium was discovered here on Earth.

By the late 1800s, most physics work related to light was being done with the understanding that light was composed of waves: in fact James Clerk Maxwell (1831 – 1879) published A Dynamical Theory of the Electromagnetic Field, in which he described the unified theory of magnetism and electricity, and along with it, described light as a form of electromagnetic wave.  So at this point, detecting the ether was one of the problems that physicists were working on.

During the 19^th century, several values for the speed of light were published: Hippolyte Fizeau (1819 – 1896) reported a result of 315,000 km/s, and Leon Foucault (1819 – 1868), improving on Fizeau’s method, published a value of 298,000 km/s.  The next worker of note is Albert Abraham Michelson (1852 – 1931), who began trying to measure the speed of light in about 1877, while an instructor at the U.S. Naval Academy.  He accepted a position as a full professor at Case School of Applied Science in 1883, and in 1887 he and Edward Morley (1838 – 1923) performed an experiment to detect the motion of the Earth relative to the ether.

The way that the experiment was designed was to have a single light source, split the beam of light from it and send one beam in the direction of the Earth in its orbit, and the other at 90 degrees from it, essentially across the motion of the orbit.  Both of the beams of light were reflected back to the same place from mirrors that were placed to be exactly the same distance from the split, and based on the interference pattern, the experiment should have allowed Michelson and Morley to determine the speed of the Earth relative to the ether.  The concept was very much like firing a cue ball at two other billiard balls, placed in a way that they would move at 90 degrees from each other, hit cushions placed so that the distances were the same, bounce back, and if they collided in the same place that they had started from, the billiard table could be considered stationary.  But if it had been done on a train, the billiard ball traveling with the direction of the train, then bouncing back, against the direction of the train, would take slightly more time than the billiard ball traveling across the direction of the train.  So at least was the theory.

Michelson and Morley got a null result – meaning that no matter how precisely they could measure it, there was no effect on light from traveling through the ether.  Michelson continued to make improvements on his equipment, and still could not determine the effect of the ether.  He did provide more and more accurate measurements of the speed of light, over time, with his final determination while he was alive being 299,706 ± (meaning plus or minus) 4 km/s.  He made this measurement in 1924 in California, after the U.S. Coast and Geodetic Survey had taken two years surveying an accurate baseline for projecting light: the precise distance between Mount Wilson Observatory and Mount San Antonio, about 22 miles away.  The survey, no doubt, used some of the instruments discussed in the earlier posts about geodetic surveys.  He set up his last experiment, but did not live to see the results: published posthumously as 299,774 ± 11 km/s.

The next big player was Albert Einstein.  His own reports conflict about whether he knew of the Michelson-Morley experiments results, though it is clear that he knew about the formula developed by Hendrik Lorentz (1853 – 1928)  which was created in response to the Michelson-Morley experiment, known as the Lorentz contraction.6

Einstein was less concerned with the precise speed of light than with the concept of pure energy waves traveling very fast.  In an autobiographical statement, he described how he came to understand light, which has been picked up by the physics community as the archetype of a gedankenexperiment – a thought experiment.  He imagined traveling with a light beam at the speed of light.  What he determined he would be able to see was contradictory to both experience and to Maxwell’s equations about electromagnetic waves, but only if time was considered to be absolute.

After ten years of reflection such a principle resulted from a paradox upon which I had already hit at the age of sixteen: If I pursue a beam of light with velocity c (velocity of light in a vacuum), I should observe such a beam of light as a spatially oscillatory electromagnetic field at rest.  However, there seems to be no such thing, whether on the basis of experience or according to Maxwell’s equations.  From the very beginning it appeared to me intuitively clear that, judged from the standpoint of such an observer, everything would have to happen according to the same laws as for an observer who, relative to the earth, was at rest.7

In other words, light could never be at rest, and even for an observer traveling at the speed of light, an impossibility, light would still have to appear to be moving at the speed of light.  The result of his thought experiment was the conclusion that the speed of light is absolute, a universal constant, that nothing with any mass could ever be accelerated to the speed of light, and nothing could ever exceed it.  Oh, and by the way, there was no need to talk about the ether.  Most likely, it didn’t exist.

This concept is only part of the weirdness Einstein left us with.  The other part was his realization that energy was not continuous.  Energy came in very small bundles, but could not be split down smaller than a single one of these bundles, called a photon.  And that light behaves like a particle when the experiment is set up to measure particle-like behavior and it behaves like a wave when the experiment is set up to measure wave-like behavior, since it is, in fact, both.

These two concepts were major changes in the way that light is understood.  The consequences of this new set of concepts are so many that it would take (actually has taken) years to fully elucidate them, and there may still be surprises left.

However, to wrap this up, the speed of light, then, as a constant continued to be measured against the standards that had been defined here on earth: the second, distance in terms of meters or miles, etc., until 1983.  In 1972, the U.S. National Bureau of Standards measured the speed of light in a vacuum to be 299,792,456.2 plus or minus 1.1 m/s (notice that this is meters per second: move the decimal point three places left for kilometers/sec).  In 1975, the 15^th Conference Generale des Poids et Mesures (CGPM) set the value at 299,792,458 m/s.  Then in 1983, evidently the 17^th CGPM changed the way that a meter was defined: it used the speed of light to define the length of a meter as “The metre is the length of a path travelled by light in a vacuum during the time interval of 1/299,792,458 of a second”8

So, by measuring light and re-conceptualizing it, light has become the standard length by which all other length systems are now measured.  Who else saw that in the refraction from the prism/clock?  Go ahead, raise your hands.

Sources relied on for this post are:

Albert Einstein: Philosopher-Scientist, The Library of Living Philosophers, Volume VII, Schilpp, Paul Arthur, ed. Open Court Publishing Company, La Salle, Illinois, 1949, 1951, third edition, fourth printing 1988.

Asimov, Isaac, Understanding Physics: Light, Magnetism, and Electricity, New American Library, New York, N.Y., 1966.  Volume II of three, an old source, but clear, accurate and helpful.  And you thought Isaac Asimov only wrote science fiction?

Freely, John, Aladdin’s Lamp, How Greek Science Came to Europe Through the Islamic World, Alfred A. Knopf, New York, 2009.  Good discussions of the Greek science, and an extensive run-through of the work of the Islamic scientists and scholars.

Isaacson, Walter, Einstein, His life and Universe, Simon & Schuster, New York, N.Y., 2007.  A thorough and warm biography, with a great quote from Einstein after the dedication: Life is like riding a bicycle.  To keep your balance you must keep moving.

Rubenstein, Richard E., Aristotle’s Children, How Christians, Muslims, and Jews Rediscovered Ancient Wisdom and Illuminated the Dark Ages, Harcourt, Inc., Orlando, FL  2003.  With the focus on the transmission of Aristotle’s works, detail about other aspects of the Islamic custodianship of knowledge is just skimmed over.

And the ever-present, really convenient Wikipedia.

---

1 http://en.wikipedia.org/wiki/Speed_of_Light

2 http://en.wikipedia.org/wiki/Speed_of_Light

3 At the time that Isaac Newton was born, the Julian calendar was in use in England, and his birth date was December 25, 1642.  On the Gregorian calendar, later adopted by England in 1752, the date was January 4, 1643.  I prefer to provide cover for all those atheists and others of little faith to have a reason to celebrate on the 25^th of December.

4 Asimov, Isaac, Understanding Physics: Light, Magnetism, and Electricity, New American Library, New York, N.Y., 1966. p.67

5 Asimov, Isaac, Understanding Physics: Light, Magnetism, and Electricity, New American Library, New York, N.Y., 1966. p. 68.

6 Strictly known as the Lorentz-Fitzgerald contraction: George F. FitzGerald (1851 – 1901) did the initial work in 1889 as a result of the Michelson-Morley experiment, and the formula was more fully developed by Lorentz in 1892.

7 Einstein, Albert, “Autobiographical Notes” (in German, and in English translation) in  Albert Einstein: Philosopher-Scientist, The Library of Living Philosophers, Volume VII, Schilpp, Paul Arthur, ed. Open Court Publishing Company, La Salle, Illinois, 1949, 1951, third edition, fourth printing 1988.  p. 53.

8 “Resolution 1 of the 17^th CGPM” ( http://www.bipm.org/en/CGPM/db/17/1/ ), as quoted in http://en.wikipedia.org/wiki/Speed_of_Light

Surveying and Statecraft II or ” The empire exists because it can be mapped”

In the last post, I discussed surveying boundaries and used the Mason-Dixon line as the example.  In this post I will discuss another form of statecraft that has been attributed to geodetic surveying: domination.  I suspect that using geodetic surveying to establish domination may be a glorified form of cadastral surveying – the surveying to establish property boundaries between property owners – and that it may have been done in other settings than the example I will use: the Great Arc surveying of India by Britain.  However, cadastral surveying can be performed using theodolites and chains only, while to perform the survey of India, astronomical techniques of establishing longitude and latitude were necessary as well as triangulation.

To understand the effect of the geodetic survey of India, one must know some of India’s history.  India has been known since classical times.  Eratosthenes (276 to 194 BC) mentions it and may even have drawn a map which included it.  The map shown in my post, “Virtual Lines”, was a late-medieval re-creation of a map, probably based on text by Eratosthenes that survived.  Both the Indus and the Ganges Rivers are shown the map, and the eastern most boundary of land is the eastern edge of India.  By the time of Strabo (c 63 BC to c 24 AD), land to the east of the Ganges shows up on a late reconstruction of his map, with everything east of the Ganges river is referred to as “India extra gangem”, while the area between the Indus to the Ganges is labeled “India intra gangem”.1 Tales about “the Indies” ranged from fabulous to outright fable – strange lands filled with strange and exotic people, and places to find spices, silks, teas and other unobtainable luxury items.

From pre-history, the land that would become India has been populated with people following a number of religions – principal among them are Hinduism and Buddhism, with significant other beliefs, sects and religions.  The areas were broken up among various local kings and rulers, with little, if any, overall coordination.  The Moslem conquest of India began around 1200, and resulted in Moslem rulers, sultans, controlling varying sized areas.  Each sultan’s dominance was dependent on the sultan’s ability to conquer and maintain his grasp.  The sultanates were unstable: a majority of sultans left office having been assassinated.  The Mogul (Mughal) conquest began in 1526, spread throughout the sub-continent, and was stable for nearly 200 years.  By 1700, the Mogul Empire was at its largest: in the north, it included Kashmir; to the west, Balochistan was included; the east extended to and included Bengal; and in the south, the Kaveri basin, leaving only a small area at the southern tip and Sri Lanka not under Mogul control.  “Following 1725 the empire declined rapidly, weakened by wars of succession, agrarian crises fueling local revolts, the growth of religious intolerance, the rise of the Maratha, Durrani, and Sikh empires and finally British colonialism.”2

European interest in the Indies in the late middle ages was driven by the hope of finding sea routes to sources of goods from the East, and being able to replace the supply chain of Arab traders and Venetian merchants.  The interest was expressed by Portuguese voyages of discovery in the 1400s, leading to the successful rounding of the Cape of Good Hope and establishment of trade with the lands finally reached.  A side effect of this was, of course, Christopher Columbus’s inadvertent discovery of a continent blocking his voyage to the Indies.

The English joined the trading competition somewhat late: the charter of the East India Company, representing London merchants, was granted in 1600 by Queen Elizabeth I, and the next hundred years were spent setting up places to trade in “the Indies”, competing with other European countries such as the Portuguese, Dutch and French.  In 1615, a diplomatic mission sponsored by King James I succcessfully negotiated a commercial treaty with the Mogul Emperor, Nuruddin Salim Jahangir, permitting the Company to set up a “factory”, a trading post, in Surat, just up the coast from Bombay.  In 1670, after the restoration of the monarchy in England, King Charles II amended the charter to include the right to acquire territory, mint money, command fortresses and troops, make war and peace, and administer civil and criminal authority over their territorial acquisitions.

By 1700, the East India Company had established a number of factories, but their main three trading centers were in Bombay, Madras, and Calcutta, which were operated as essentially independent entities:

• Bombay is now Mumbai: on the western side of the sub-continent, just under half way up the coast from the southern tip.
• Madras: near the southern tip on the eastern side, across the straits from Sri Lanka/Ceylon.
• Calcutta is now Kolkata: on the eastern side in eastern West Bengal.

Below is a link to the Google Map of India. You may have to zoom in a bit to see all of the cities mentioned above.

http://maps.google.com/maps?f=q&source=s_q&hl=en&geocode=&q=India&aq=&sll=37.0625,-95.677068&sspn=49.844639,61.083984&ie=UTF8&hq=&hnear=India&ll=20.097206,77.255859&spn=29.508738,30.541992&z=5

In 1708, there were a few more changes: other English merchants wanted to participate in the India trade, and after those merchants formed an association, the East India Company merged with the new association, changing the charter to represent English, as opposed to just London, merchants.  1708 was also the year of the Act of Union between England and Scotland, and after that was ratified, the English East India Company became known as the British East India Company.

The trading rivalry between Britain and France became more intense in the 1700s, at the same time that the turmoil in the Mogul Empire began the process of dissolving the authority of the Mogul Emperors.  Evidently, during this time, both Britain and France sent troops, ostensibly to protect their trading investments, but both rented regiments to Indian princes.  Soon, the British were managing the princes’s finances directly.  The competition between Britain and France culminated in the Seven Year’s War (1756 – 1763), which extended to all of their territories (see the last post’s mention of the French and Indian War on the North American continent).

It was about this time that a British army under Robert Clive (the legendary “Clive of India”) attacked and defeated the Nawab of Bengal at Plassey (1757), which led to the East India Company governing Bengal.  There were further territorial gains, and some unfortunate financial reverses for the Company which led to the India Act in 1784, changing the Company’s relationship with the British Government from a mercantile entity to a territorial power, under the control of and supported by the British Government.

We can now look at the surveying done by the British.  In 1764, James Rennell received a commission in the Bengal Engineers as a surveyor for the East India Company.  Clive was impressed with his work, and promoted him to Surveyor-General in 1767.  Rennell was wounded during an action in 1776, retired from active service in 1777, and returned to England to work on geographical matters at East India House in London.  In 1782, he issued his first map, titled “Hindoostan”, and titled his memoirs “Memoir of a Map of Hindoostan; or the Mogul Empire”.  The map included all of the sub-continent, and while he referenced Hindoostan, in his memoir, he used the term “India” as if it were interchangeable with the Mogul Empire.

In his very thorough and intelligent book, Mapping An Empire, Matthew H. Edney describes the overall effort of mapping of India by the British:

In the case of the British conquest of South Asia in the hundred years after 1750, military and civilian officials of the East India Company undertook a massive intellectual campaign to transform a land of incomprehensible spectacle into an empire of knowledge.  At the forefront of the campaign were the geographers who mapped the landscapes and studied the inhabitants, who collected geological and botanical specimens, and who recorded details of economy, society, and culture.  …the geographers created and defined the spatial image of the Company’s empire.  The maps came to define the empire itself, to give it territorial integrity and its basic existence.  The empire exists because it can be mapped; the meaning of empire is inscribed into each map.3

The mapping started with Rennell and continued, with surveyor-generals operating out of each of the three British trade centers, and then centralized in the Great Trigonometric Survey in 1802.  The plan was to survey both longitudinally and latitudinally, and was originally projected to take 5 years.  That was a bit too short by, roughly, 70 years.  Work was still being done by the GTS as late as 1876, and may have continued longer than that.  However, the Great Arc, the longitudinal survey, 1600 miles, was completed in about 1843, at which point, the Superintendent of the GTS and Surveyor-General of India at the time, both positions held by George Everest, packed up and went back to England.  In the following illustration, the map of India is overlaid with the triangulation paths of the GTS and other surveys.4

In a book named The Great Arc, John Keay details the trials and travails of the surveyors.  Evidently in addition to a climate to which they were not accustomed and in which they suffered from fevers, malaria, and other tropical physical indignities, they encountered hostility, not too surprising, from the indigenous people, and other perils such as tigers, scorpions, floods, etc.  They were very tough, and moved from surveying site to surveying site with heavy Ramsden theodolites and repeating circles, none of which had the portability of the French repeating circles.

Did they know what they were doing beyond the surveying?  Absolutely.  Everest, in his first expedition, put down a mutiny and publicly flogged several of the natives whose services had been “lent” to him by the local Nizam-ul-Mulk, the Administrator of the Realm.  He evidently felt that having his authority questioned put the entire presence of Britain in India at risk.

The history is much more complex than I can describe in this short post, though dominance was clearly the main theme of the British with exploitation a close second.  Some of India was conquered by military force, some by negotiation, and some by performing indispensable services, like managing the finances for local authorities – in essence, taking over the exchequer – then taking over the rest of the government.  The financial benefits to the Crown were enormous, ranging from taxes to tributes, cheap labor, the monopoly of the tea trade, etc.  All of it was supported by the surveyors, defining the land, as much for effective taxation as for military advantage.  The surveyors used surveying techniques we have already discussed.  No new techniques were developed, this remained an engineering problem, as well as a survival problem.

New discoveries were only of what was there, geographically, most of which was already known by those who had preceded the British.  There are some impressive geological features that were discovered, such as the Deccan Traps, volcanic lava that consists of “…multiple layers of solidified flood basalt that together are more than 2,000 m (6,562 ft) thick and cover an area of 500,000 km² (193,051 sq mi) and a volume of 512,000 km³ (123,000 cu mi).”5 There was a quest to find the headwaters of the Ganges – not the longest or largest river in the world, but worthy of exploration nevertheless.  And of course, Chomolongma was “discovered” during the Great Arc surveying, and the British renamed it “Mount Everest” as a tribute to “worthy” George Everest, flogger of natives.

The action in the novel, Kim, by Rudyard Kipling, published in 1901 and set in about 1888, a little after the surveys were mostly completed.  But in the story, Kim becomes an operative of a British spy network run by the head of the Ethnological Survey, Colonel Creighton.  Education is arranged for Kim, so that he can be trained as a surveyor, with a compass and a measuring chain.

The great game, as it is called in the book, the contest between Russia and England for dominance in the Northwest region of India, required surveyors, and one of the uses to which Kim, the character, is put is to recover the surveying notes of a pair of Russians.  Kim and friends are successful at separating the Russians from their baggage, the native baggage carriers are given permission to split up all of the baggage and provisions amongst themselves, while Kim retains the one basket that has their notebooks in it.  He searches through the basket and discards everything he doesn’t need or want to carry out of the mountains:

“The books I do not want.  Besides, they are logarithms – Survey, I suppose…The letters I do not understand, but Colonel Creighton will.  They must be kept.  The maps – they draw better maps than me – of course. …The rest must go out of the window.”  He fingered a superb prismatic compass and the shiny top of a theodolite.”6

And out the window goes everything except the letters and maps that Kim kept, theodolite, compass, books, dropped down a thousand foot cliff into an impenetrable forest.

In the story, Kim is the son of an Irish soldier and an Irish mother, both deceased.  The advantage of being a “sahib” plays in his favor in a number of ways: he is described as a clever lad due, no doubt, to the “inherently greater intelligence” of a person of European parentage, and once others know he is a “sahib”, they help provide him with a path to success.  There are other themes and strains within the book, but the reader is never allowed to forget that Kim is different than the “natives”.  The educational opportunities for the natives who work for the GTS were such that they could taught to perform the mechanical operations, essentially provide the data, but were not taught the mathematics necessary to reduce the data to information.

The Great Trigonometrical Survey and, indeed, the whole mapping enterprise were significant for the ideological image of geographical space that they created.  More than a network of astronomically determined places ever could, the trigonometrical surveys held the promise of a perfect geographical panopticon.7 Through their agency, the British thought they might reduce India to a rigidly coherent, geometrically accurate, and uniformly precise imperial space, a rational space within which a systematic archive of knowledge about the Indian landscapes and people might be constructed.  India, in all of its geographic aspects, would be made knowable to the British.  The British accordingly constructed the Great Trigonometrical Survey as a public works which could not be undertaken by the Indians themselves, but which was as concrete and as necessary as irrigation canals and military roads for pulling together, improving and defining India and its inhabitants.  And the spatial significance of the trigonometrical surveys was inscribed into the maps the British produced.  They defined India.8

.

This, then, shows a completely different side of performing geodetic surveying:  in support of statecraft and domination.  While measurement itself is based on scientific and mathematical concepts, the use to which the results are put comes a surprise, perhaps.  At a deeper level, one of the reasons to measure and reason about the world has always been to control – though usually the control is thought of as control of the material world or the environment rather than the world of human relations. But that thought opens other doors, for other posts.

---

1 Brown, Lloyd A., The Story of Maps, Dover Publications, Inc., New York, N.Y. 1949,1977. The map attributed to Eratosthenes is on p. 51, and that attributed to Strabo is on p. 56.

2 http://en.wikipedia.org/wiki/Mughal_Empire

3 Edney, Matthew H., Mapping An Empire, The Geographical Construction of British India, 1765 – 1843, The University of Chicago Press, Chicago, Ill. 1990, 1997. p. 2.

4 Keay, John, The Great Arc: The Dramatic Tale of How India Was Mapped and Everest Was Named, Perennial/HarperCollins Publishers, New York, N.Y., 2000, 2001.  Following p. 76.  Credit is given to C.R.Markham, Memoir of the India Survey (c. 1870).

5 http://en.wikipedia.org/wiki/Deccan_Traps

6 Kipling, Rudyard, Kim, Penguin Books, London, England. 1989.  Originally published in 1901, the volume that I have is based on the American Burwash Edition, 1941, with Kipling’s final revisions.  The introduction is by Edward Said.

7 “panopticon”, as used by Edney, is defined as an “instrument… of permanent, exhaustive, [and] omnipresent surveillance”.  p. 24.

8 Edney, Matthew H., Mapping An Empire, The Geographical Construction of British India, 1765 – 1843, The University of Chicago Press, Chicago, Ill. 1990, 1997. pp.319-320.

Surveying and Statecraft I

In several earlier posts, I discussed maps, map-making, surveying, and the tools and concepts necessary for the accurate measurement of land and geography to create accurate maps.  Along the way, I’ve mentioned cadastral (i.e. real estate) mapping, but mostly I’ve talked about mapping the shape of the Earth and the shape of its lands, called geodetic mapping, which requires a reference scheme (longitude and latitude), geometric concepts and the tools to use the reference scheme and concepts.  Greater accuracy in the tools developed over time, as well as some standards for the procedures for using them.

One function of surveys that I have not yet covered has been the setting of boundaries: not necessarily the boundaries between two or more properties, but between two politically different entities.  Who set the boundary between France and Belgium, or between Belgium and the Netherlands?  Was the boundary established via a survey?  Actually, no: most boundaries were established by treaty and were specified in words, but I can only find mention of surveys in a very few cases.  The words in the treaties lay out what the boundaries are, in some cases, such as defining a border as a specific river, the political entities on each side being granted half.  In many cases, natural geographical features were used as boundaries, such as the water around the British Isles delineating the U.K. from the rest of the world.  Setting borders is not measurement leading to discovery: instead, it is a form of engineering using standards and specifications to perform measurements, and results in something more or less useful.

One boundary that I know was put into place by a survey divides Pennsylvania and Maryland with the Delaware separated from both of them.  This was done by a survey led by Charles Mason and Jeremiah Dixon – the Mason-Dixon line.  I admit that I never thought about it very much until the novel by Thomas Pynchon came out, called Mason & Dixon.  I read the book, enjoyed it, and have wondered how factual the story that Pynchon wrote was or is.  Short of re-reading, it, though, I suggest that much of it is based on fact, since I know that Pynchon is reputed to be a thorough researcher, though there is plenty of room of Pynchon’s creative invention.

The genesis of the conflicting claims has to be laid to the way that both the colonies received their charters.  The first, the charter for the Maryland colony, was given to the 2^nd Lord Baltimore, Cecil Calvert, though the idea of it and its boundaries had been proposed by his father, George Calvert, the 1^st Lord Baltimore, who died shortly before it was granted in 1632.  The Calverts were Catholics in Anglican England, and George had proposed the colony to be a refuge for Catholics: essentially a way to put the “Catholic” problem out of sight and thus out of mind.  The supporters of the already established colony of Virginia were not pleased by this, and they lobbied, mostly unsuccessfully, to eliminate the new colony.  They were only successful in having the charter changed to reflect the fact that Virginia settlers were already in part of the territory originally granted to the Calverts.

While Cecil stayed in England to fight the Virginia challenge, he sent his younger brother, Leonard, to establish the colony and be its first governor.  In the instructions that Cecil gave Leonard, he stressed that the colony needed to be established with religious tolerance as part of its principles, since the colonists originally sent were both Catholic and Protestant.  In 1649, the assembly of the Maryland colony passed the first law requiring religious tolerance in the British colonies.

The establishment of the Maryland colony occurred during upheavals in England: in 1629, the King dissolved Parliament, the apparent start that undermined the stability of England, led to the three civil wars, the beheading of King Charles I, the dictatorship of Oliver Cromwell, and ultimately to The Restoration in 1660.  A pretty tough 30 years or so for England, throughout most of which and at the end of which, the Calverts retained their proprietorship of Maryland.

The other charter, that of the area known as Pennsylvania, was granted to William Penn in 1681.  It, too, has a background story: William Penn’s father, Admiral William Penn, had rendered services and financial backing to the restored monarchy, so despite young William’s radical Quaker faith, his arrests for proselytizing, etc., not only the King, Charles II, but the Duke of York, who became King James II at the death of Charles II, gave up territory for the charter.  William, being a theological visionary with his head in the clouds, as it were, was not so well grounded that he paid close attention to the boundaries, and despite his charter granting him lands above the 40^th parallel, established the city of Philadelphia below the 40^th parallel.  In Wikipedia, there is a wonderful map showing the approximate overlap of the two charters, as envisioned by the protagonists.1

The Maryland charter was supposed to cover all the land north of the Potomac River up to the 40^th parallel, on both sides of Chesapeake Bay, east to Delaware Bay and the Delaware River.  I have not discovered how the western border was specified.

The Pennsylvania charter was to be the land north of the 40^th parallel from the Delaware River, south of New York and its western border was specified as a longitudinal line 5 degrees from the Delaware River.

For some reason, the three counties in the eastern part of the Maryland charter ended up as part of the Pennsylvania charter.  They did not remain there for too long, though, since the settlers expressed a desire to be independent almost immediately after the new proprietor of Pennsylvania arrived, and were granted semi-autonomy in 1704.  The town of New Castle in what became Delaware was the first established city in the region, and its borders figure in to the eventual settlement and surveying.

The dispute between the Calverts and the Penns remained unsettled,  and led to violent clashes between settlers of both loyalties.  It should be noted that the Pennsylvania charter area maintained religious tolerance, much like that put into law by Maryland, but Pennsylvania attracted disaffected and persecuted people from throughout Europe as well as from England, while it appears that Maryland mainly attracted English settlers.

In 1732, the 5^th Baron Baltimore signed a provisional agreement with Penn’s sons, agreeing to a line between the colonies and giving up the claim to the three counties of Delaware, but later, he denied that the document had some of the terms he had agreed to.  In 1750,  a royal commission was set up, and one of the results was that in 1760 the Crown ordered the 6^th Baron Baltimore to accept the 1732 agreement.  (Seems like it was a good time for the British to establish clear boundaries in North America: the date nearly matches the end of the French and Indian war: Quebec conquered in 1759, Montreal capitulated in 1760, and the Treaty of Paris signed in late 1762.)

The resulting agreement specified the following:

• Between Pennsylvania and Maryland:
  • The parallel (latitude line) 15 miles (24 km) south of the southernmost point in Philadelphia, measured to be at about 39°43′ N and agreed upon as the Maryland–Pennsylvania line.

• Between Delaware and Maryland:
  • The existing east-west Transpeninsular Line from the Atlantic Ocean to its mid-point to the Chesapeake Bay.
  • A Twelve Mile (radius) Circle (12 mi (19 km)) around the city of New Castle, Delaware.
  • A “Tangent Line” connecting the mid-point of the Transpeninsular Line to the western side of the Twelve-Mile Circle.
  • A “North Line” along the meridian (line of longitude) from the tangent point to the Maryland Pennsylvania border.
  • Should any land within the Twelve-Mile Circle fall west of the North Line, it would remain part of Delaware. (This was indeed the case, and this border is the “Arc Line”.)2

The resulting line between Pennsylvania and Maryland follows the parallel at approximately 39 degrees 43′ N, depriving Maryland of about 17′ worth of land.

Charles Mason and Jeremiah Dixon led the survey, many of the details of which are found with embellishments in Pynchon’s Mason & Dixon.  They started in 1763 and finished or stopped in 1767.  Mason was an astronomer, and Dixon, a surveyor, which, based on the information I discussed in the earlier posts about geodetic surveys, seems like the appropriate mix of skills.

How does their measurement function for statecraft?  Violence ceased between the two sides about the location of the border, but after they finished, the border came to symbolize not just the difference between Maryland and Pennsylvania, but the divide between the colonies that permitted slave-owning to the south and those that eschewed slave-owning in the north.  While Penn himself did own and trade slaves, in his will, he granted his slaves their freedom upon his death.  There were Quakers, though, who were more opposed aggressively to slavery, and led Pennsylvania to outlaw slavery in 1781.  Obviously, measurement did nothing to contribute to or to oppose slavery, but it did provide a convenient demarcation between the territories.

In the work that Mason and Dixon did, they marked each mile with stones, and every five miles placed a crownstone – a vertical stone with four sides, with the Penn family coat of arms on the side facing Pennsylvania and the Calvert family coat of arms facing Maryland.  Mason and Dixon ran their latitude line dividing Pennsylvania from Maryland for about 244 miles, but apparently were stopped short of completing the 5 degrees by hostile Native Americans.  That job was completed in 1784 by other surveyors.

As a somewhat peculiar consequence to the job done by Mason and Dixon, their results appear to have triggered a completely different type of geodetic measurement, one beyond the engineering of borders.  To check the accuracy of surveys of this sort, after completing the line in one direction, the surveyors repeat their procedures going back to the original starting point, and expect to see minor random errors.  Instead, Mason and Dixon found systematic errors that were larger than the expected random errors, and systematic in the sense that they all went in the same direction.  When they informed the British Royal Society of this, the systematic errors were recognized as a possible way to prove Newton’s theory of gravity, since the errors might be attributable to the gravitational pull of the Allegheny Mountains.  Newton had raised the possibility of mountains having sufficient gravitational attraction to pull plumb-bobs away from vertical, but ultimately felt that this would be too difficult to measure.

The Royal Society was persuaded by the Astronomer Royal of the time, Nevil Maskelyne, to follow up on this by finding a relatively isolated, symmetrical mountain and using both astronomical sightings to establish vertical, and plumb-bobs to establish at numerous points on the mountain, how much the plumb-bobs varied from vertical, to measure the gravitational pull of the mountain.  Then, using that information, the density of the earth could be extrapolated.  Maskelyn hired Mason to find a suitable mountain to use, which Mason did, but he declined further participation in the project.  The exercise was done using the mountain Mason found located in southern Scotland called Schiehallion between 1774 and 1776.

As a further aside, It seems that during the Peruvian adventure of the French geodeticists, they had tried the same kind of measurement using a volcano near Quito, Chimborazo, had found a deflection in their plumb-bobs of about 8 seconds of arc, but were unable to draw any conclusions other than that this proved that the Earth was solid, not hollow.

During the data gathering phase of the project, surveyors took thousands of bearings around more that a thousand points at various elevations on the mountain.  A mathematician named Charles Hutton was given the task of crunching the data.  To make sense of it, he drew lines connecting the points at the same elevations on the mountain where the bearings were taken, depicting for the first time the contour lines now used in relief maps.  The results of his work were twofold: one, Newton’s theory of gravitation was proven to be correct; and two, a figure for the density of the earth of 4500 kilograms per cubic meter was derived, which is less than 20% less than the currently accepted figure of 5515 kilograms per cubic meter.

Measuring the density of the earth has little to do with statecraft or the engineering of borders to provide useful definitions of proprietorship.  From the dates, it will be noticed that the measurement of Schiehallion occurred at about the beginning of the rebellion of the colonies, as described by the British at the time, which those of us in the United States call the American Revolution.  The Mason-Dixon line had settled one conflict, with greater conflicts to come based on its location and symbolic meaning, but not because a measurement had been performed.  Boundary disputes have led to war and violence far too often, and are usually settled when one side prevails, or when the combatants are exhausted, specified in treaties, with surveying that may be done somewhat afterwards.  But that is not always the case, and the next post will discuss a measurement that led not just to violence, but colonial domination.

---

1 http://en.wikipedia.org/wiki/File:Marycolony.png

2 http://en.wikipedia.org/wiki/Mason-Dixon_Line

Measuring Learning

Over the past year or more, I have read  a number of disturbing stories of school districts firing teachers and closing whole schools, for under-performing, as well as stories of school districts that have found and fired teachers who have contributed to cheating, as unintended (or perhaps intended) consequences of No Child Left Behind (NCLB).  This has been a springboard for me to reflect on my own schooling: remembering teachers, tests and testing and how and when I really learned.

As it has been quite a while since my early grade schooling, grades 1 through 5 finished in 1956, I remember very little.  I have tried to recall my teachers – of the five homeroom teachers, I remember the names of only three, and can picture only one in my mind.  As to my attitude about tests, I don’t remember having one – that is, I probably did, but I don’t remember what the testing was like, and certainly don’t know if it was different or the same as the testing today.  I do remember class sizes being small, and feeling like some of the teachers augmented my parents’ teaching and examples, not as surrogate parents, but as additional people who cared about and for me.

My sister has “helped” me in my recall effort.  Unsolicited, she sent me my kindergarten report card, a document that can only be described as embarrassing.  In it, I was reported as: “knowing [my] name, address and telephone number; counting to 25; knowing the days of the week; singing in tune; carrying out directions; and being kind polite and thoughtful.”  Oh boy!  No longer completely accurate – I can still count to 25 though – but what a set of metrics.  She also sent a couple of links to YouTube videos done by someone about my grade school containing their home movies from that time, with sentimental music and content that would only reach someone who had been there.  But none of this has helped to spark a recollection about testing and about teacher quality.

From 6^th grade to 8^th grade, I went to a junior high school, and remember a number of teachers from there.  6^th grade homeroom was led by a teacher who, 4 years later, had a psychotic breakdown in front of my brother’s class, driven by the younger brother of one of my friends.  Oh well.  When I had him, he presented bogus, frightening, paranoid information that gave me nightmares for years.  I was and still am wholeheartedly in favor of the prodding that led to his breakdown.  He will remain nameless.

I assume that the testing that was done was largely multiple-choice and short answers, but I don’t have a way to verify that.  I do remember developing an aversion to tests at about that time, with the usual student sweaty palms, tightening of the chest, heart beat speeding up, etc., when it came time to perform even as insignificant a test as a short quiz.

The next year was equally awful, but for entirely different reasons.  I was having some relationship difficulties with my peers, most likely due to the onset of hormonal changes, so I dealt with them by pleading sick a lot and missing school as a result.  My homeroom teacher, whose name is engraved deeply in my memory, was alternately understanding and pissed off at me.  I did something early in the year, relative to the grading process, that set us up against each other.  He had a requirement that every two weeks, we had to turn in a book report on something we had read.  Innocently, I had begun reading War and Peace, and he mocked my ability to read it and understand it.  To cap off his mockery, he said that if I finished it and did a book report on it, he would let me miss the deadline for several weeks, and then give me credit for the entire year’s worth.  Well, I did finish, I did understand it, mostly, and I did a long book report on it that must have been sufficiently coherent for him to honor his challenge.

The result was that he made cracks about me “beating the system”, and how I should turn in more for the rest of the year.  Publicly.  But I was unashamed, and never turned in another one.  However, I did continue reading, and gave him evidence of that.  I missed tests, because I was “sick”, and made them up, with the usual sweaty palms.  And this was about the time that we began to have essays as part of the testing procedures.

His name, as I said, is deeply engraved in my memory, and he is perhaps the only teacher before high school that I would ever want to get back in touch with to thank.  When I think about the lessons I learned that year, they had more to do with my character than any else: I feel that I have more understanding of others, and more “grit” for the handling the adversity as a result.  He never yelled at me, he mostly joked, mocked and cajoled me into being a much better and stronger person by the end of the year.  He is the only teacher that I remember that I did not want to fail in my life after school, not because I wanted to go back and rub success in his face, but because I wanted to be able to show him how much he had helped me, whether intentionally or not.

I was comfortable with tests by the time of 8^th grade, because I knew how to cram for multiple choice tests.  I was a good test taker because I had figured out the basics of the system, and had only to apply it to each teacher’s particular style or method.  Essays were harder, but I was fairly fluent and could provide enough relatively intelligent verbiage to get by.

After taking a stroll through my recollections of grades 1 to 8, I find myself questioning the sense of the NCLB act and implementation.  I don’t believe that any of the teachers I had were really all that bad, with the exception of the 6^th grade nut-case.  Would NCLB have highlighted his deficient psyche?  I doubt it.  Would any of the NCLB testing have identified the high quality of my 7^th grade teacher?  I doubt that as well.

I feel a bit like Garrison Keillor describing Lake Wobegon, where all the kids are above average.  My teachers were all “above average”?  I doubt it, but I have rarely experienced teachers who entered the profession because it was their last choice job option: most appeared to be sincerely interested in teaching their chosen subjects, and more importantly, appeared to care about the students – well, with a few exceptions, but those kids were usually discipline problems or disruptive students – this was long before the days of Ritalin-drugging kids into a quasi-receptive stupor.

Multiple choice, short answer, matching types of questions may have some validity for standardized testing, to see how much, if any, of the water in the trough has been drunk by the horses.  More than anything, such testing seems to me to be useful in making sure that students have been exposed and are absorbing the “facts” which are important for the foundation of thinking, and also for diagnosing failures to absorb them.  However, it does not in any way test whether a teacher has neglected their duty to provide those facts.  I only remember taking three “standardized” tests, but not until high school, when I took the PSAT, once, and then the SAT twice.

A distinction must be made between the standardized tests and what I learned to take tests with multiple choice, short answer and matching types of questions that were done created by my teachers.  In my cramming for these types of tests, I would go over my notes to see which “facts” were mentioned, to see what was important.  But to make sure that I had my understanding correct, once the important ones were identified, I would go to the textbook, because if I had to dispute a wrong answer, almost any of my teachers would have used the textbook either to show me the correct answer, or to accept the textbook answer in favor of one of their own.  Needless to say, almost always, their answer matched the textbook, but once or twice over the years, I was able to improve a test grade by showing how I had gotten the answer from the textbook that had been “incorrectly” marked as wrong.

With the standardized tests, the method was somewhat different, reading the preparation material, taking a big deep breath at the start, and just doing what I could.  This meant using knowledge of answers in many cases, and process of elimination and informed guessing in others, since there was no chance of an appeal, only the chance to try again, hoping to raise the score (which I didn’t).  But I was responsible for the results.  None of my teachers could have been individually faulted or targeted as being at fault for my mistakes or omissions.

A little background about NCLB.  I do have a collection of newspaper columns and articles that discuss some of the effects attributable to NCLB, but for the basic information, I found a book by Diane Ravitch to cover what NCLB is, how it is being used and what the effect has been on education.  The book is titled: The death and life of the great American school system, how testing and choice are undermining education. The title gives away her perspective, she finds NCLB to be destructive of education.

NCLB was intended by Congress to make school districts and teachers accountable for the results of their efforts.  While this sounds like a laudable goal, the way that the bill was constructed and the way that it is being implemented has damaged school systems and education around the country.  The major points are:

• Each state chooses the tests that they will use, defines three levels of performance, and determines what proficiency is for the tests.
• Schools receiving federal funding must test English and Math proficiency each year for grades 3 to 8, and once in high school, and separate the test results by ethnic group, race, family income, etc.
• All states must reach 100% proficiency in their teaching by 2013-2014.  Based on that, the states have set up timelines for achieving 100% proficiency in English and Math, and must show “adequate yearly progress”, AYP, based on their timelines, toward achieving the goal.
• There are strict sanctions laid out for schools and school districts not reaching AYP each year, and very severe sanctions for not reaching the goal in 2013-2014.  The main reward was to have funding continued so that the school and school district could continue to function the way that it had.
• All states must also participate in the National Assessment of Educational Progress (NAEP) standardized test on English and Math, delivered in 4^th and 8^th grades every other year.  The NAEP results are to act as an external monitor of the yearly progress.1

So, NCLB lets the states determine what the test contents are, and most likely, each state will use their own standardized test.  They determine what is considered “proficient”, and they determine their AYP.

While a standardized English or Math test, delivered with multiple choice, short answer, and matching types of questions may provide some insight into the proficiency levels of students, it is hard for me to believe that such a test will really determine how well a teacher has performed – this is too indirect, and there are far too many ways to “game” the system.  Additionally, there are many more factors that determine the performance of students on tests and teachers in classrooms than this method considers.  Yet careers are being destroyed, and workable schools dismantled based on NCLB, without any metric showing educational gains as a result.  In Ravitch’s book, she shows examples of schools and school districts that have registered impressive AYP while the scores on the NAEP have been flat, showing no gains and some losses over the same periods of time for those same schools and school districts.

There are a number of ways to look at NCLB to realize how flawed the whole concept is.  One is to realize that the method for accountability is based on that used by businesses regarding the performance of their sales people only.  If a company’s production line ran into significant difficulties that led to a decline in the quality of their products, but the company ignored the declining quality and only judged their managers on their sales people’s inability to sell “junk”, they would be addressing the wrong problem.  Likewise, if a real estate company were to fire their middle management because their sales people were unable to sell any property during the financial meltdown, again, this would be to ignore what the actual problem is.  But this is the way that NCLB is being used to make teachers, schools and school districts accountable.

The goal is to measure the proficiency of the students in two subjects: using a state-wide standardized test with multiple choice answers, the numbers are gathered, and if the numbers are too low, blame the teachers, schools and school districts.  One might expect other factors to be looked at, but apparently they are not.  The test is designed to measure an individual’s proficiency, yet rolled up, it is used to measure the effectiveness of teaching.

Often, adapting the method of measuring from one discipline to another is done in a manner that misuses the methods and results of measurement.  A prime example is described in an earlier post, in which the book by Stephen Jay Gould is discussed, The Mismeasure of Man.  In what purported to be the same objective data-gathering techniques as were used in the physical sciences, the data turned out to be skewed in favor of the investigator’s biases, and the interpretation of the data was used to misjudge the potentials of people in various “sub-standard” ethnic classifications, and then limit their possibilities.

I alluded to two problems, above, the ease with which the system can be gamed and additional factors associated with testing.  I first came across the ease with which the system can be gamed in the first chapter of Freakonomics, A Rogue Economist Explores the Hidden Side of Everything, by Steven D. Levitt and Stephen J. Dubner.  Based on the description in the book, Dr. Levitt was hired to use data from standardized multiple choice testing gathered over a period of years at the Chicago School District to identify which teachers had a high likelihood of cheating by entering answers for their students.  The negative incentives for low scores among their students for teachers and schools were strict, and there were some positive incentives for high scores and improvements.  He were able to identify a number of teachers who had probably cheated, then repeated the testing of their students with monitors present, and none of the classes were able to repeat their results.  Those teachers were fired.

Entering answers for their students is a particularly egregious way to game the system: many are more subtle, as covered in Ms. Ravitch’s book.  Methods that have evidently been used in response to NCLB have ranged from teaching only to prepare for the test; excluding other subjects and other material related to the test subjects; providing students with the answers; lowering the “proficiency” standard (34% right was mentioned as the number required to be considered a passing grade in one instance); schools that were not public schools have restricted the numbers of likely low-achieving students by setting up hurdles that they cannot jump; flunking the low-performers so that they are sent to a public school to depress the public school score; even encouraging low-performers to stay home the day of the test.  She quotes something she calls Campbell’s law: “The more any quantitative social indicator is used for social decision-making, the more subject it will be to corruption pressures and the more apt it will be to distort and corrupt the social processes it is intended to monitor.”2

The final chapter in Ms. Ravitch’s book, Lessons Learned, describes what will not improve schools (NCLB is only one culprit), and provides a vision of what students should be capable of when finished with school.  It is not a prescription, rather, it is a guideline: “Students should regularly engage in the study of the liberal arts and sciences: history, literature, geography, the sciences, civics, mathematics, the arts, and foreign languages, as well as health and physical education.”3 While one might disagree with some of this, the goal of all education should be to be to turn out students who are self-reliant, able to think for themselves, and are aware of the culture in which they will be functioning.

As a person who has some of those attributes, I am challenged to figure out where and how I learned these.  Certainly not from any of the multiple choice testing I was subjected to, though perhaps learning how to cope with that sort of situation might have contributed to my overall resilience.  I am certain that my teachers deserve much credit (even the nut-case gets credit for some learning) but also my family does, for they all have always supported me (or put up with me), as do my friends, my work-mates, and my good luck.

The one class that I have always valued the most, in terms of when I learned the course subject material better than in any other, was one that I took while I was in college.  The professor had a specific set of readings that had to be done, and a rigorous set of elements that had to be learned.  For some reason, this structure set me free: I ignored some of the reading that was uninteresting to me, but followed footnotes and references in the readings that were interesting.  In the end, my grade suffered, because I had ignored some of the elements I should have learned, but on the essay questions, for the first time in my life, I enjoyed myself responding to the topics, drawing on all of my digressions (though at the time I considered it research) for my answers.  The professor did not penalize me as much as he probably could have, but that was in part because I must have intrigued him.  A result was that once the class was over, the professor became a friend and mentor for the remainder of my years in college with whom I could discuss almost anything.

Would there have been any way to measure that kind of “success”?  If my grade had been looked at, would he have suffered for my inattention and “research”?  Would it have been fair to judge him on that?  Hardly.

The books cited in this post are:

Steven D. Levitt and Stephen J. Dubner, Freakonomics, A Rogue Economist Explores the Hidden Side of Everything, HarperCollins e-books, 2005, 2006, Adobe Digital Edition September 2009,

And

Ravitch, Diane, The death and life of the great American school system, how testing and choice are undermining education, Basic Books, New York, N.Y., 2010.

Both are worth the time to read.

---

1 This list has been adapted from that in Ravitch, Diane, The death and life of the great American school system, how testing and choice are undermining education, Basic Books, New York, N.Y., 2010.  pp. 107-109.

2 Ravitch, Diane, The death and life of the great American school system, how testing and choice are undermining education, Basic Books, New York, N.Y., 2010.  p.171.  Her footnote for this quote is: Donald T. Campbell, “Assessing the Impact of Planned Social Change,” in Social Research and Public Policies: The Dartmouth/OECD Conference, ed. G.M.Lyons (Hanover, NH: Public Affairs Center, Dartmouth College, 1975), 35.

3 Ravitch, Diane, The death and life of the great American school system, how testing and choice are undermining education, Basic Books, New York, N.Y., 2010.  p. 242.

Marking Time (or at least calibrating it)

While I was reading some research material for the last post, I came across a statement that made me wonder: the statement was that the French group that went to Ecuador to measure the length of a degree at the equator, had pendulum clocks that had to be calibrated for the local version of one second.  Additionally they used their pendulums to measure the force of gravity.  The question that I came up with is, well, how did they do that?

First, calibrating a pendulum.  What would you calibrate it against?  Another pendulum that has already been calibrated?  But what would you have calibrated that one to, ad infinitum.  To understand how to calibrate a pendulum, a bit of time keeping history needs to be looked at.

So, to establish the beginnings of a “clock”, humans have relied on natural processes that happen outside of their control, that are regularly repeating events – oscillations, if you will – such as the rising and setting of the sun.  That represents the daylight portion of one day: the non-light night portion of the day is the only other portion, so that is a fairly simple oscillation to calibrate to.  How do you measure a day as a unit? You pick an arbitrary start – sunrise, sunset, midday, midnight – and each day unit is the duration between a rise and the next, or a setting and the next, etc.  A fairly simple cycle, and a likely starting place for time keeping.

What would be next?  There are some other cycles that were apparently untangled by several early cultures.  Herodotus in his Histories, Book 2, states:

As to human matters, they all agreed in saying that the Egyptians by their study of astronomy discovered the year and were the first to divide it into twelve parts…the Egyptians make the year consist of twelve months of thirty days each and every year intercalate five additional days, and so complete the regular circle of the seasons.1

However, he is not completely reliable and evidently didn’t learn from “they” about the Egyptian lunar calendar.  His informants, the “they” who “all agreed” he says were priests he questioned in Memphis, Thebes and Heliopolis.

As to how they did this, he does not address the question, but one would probably not be too far off-base by figuring that over a period of years, the pattern of the stars in the sky would have been recognized as being essentially unchanging.  Once that was figured out, counting the days between a repeat of the stellar positions would only have required some patience and diligence: one slash on a papyrus per day would do it.  By the time of Herodotus, though, this exercise had been performed by the Babylonians and the Chinese as well, for both cultures had calendars before 450 BC.

At this point we have the year roughly figured out, and the day as the unit.  How about dividing up the day somewhat finer than roughly half daylight and the other half dark?  Establishing a midpoint for the day could be done with a very simple tool: a gnomon, or a plain straight stick stuck into the ground vertically, would project a shadow that was always “longest” at the approximate middle of the day.  This way daylight could be divided into two portions of time, before “middle” and after “middle”.  The initial shadow of each day would also put boundaries on the time of daylight within a day, and would range from shorter times of sunlight in the winter to longer in the summer.  How would this time best be divided up into what would become “hours”?

Using a sundial would not necessarily suggest dividing the time of daylight or darkness into 12 portions, and I have found only one possible suggestion as to why there was such a division, rather than dividing it into, say, 4 portions or 6 portions, even 9 portions.  The suggestion comes from a Wikipedia article which I quote:

Astronomers in the Middle Kingdom (9th and 10th Dynasties) observed a set of 36 decan stars throughout the year. These star tables have been found on the lids of coffins of the period. The heliacal rising of the next decan star marked the start of a new civil week, which was then ten days. The period from sunset to sunrise was marked by 18 decan stars. Three of these were assigned to each of the two twilight periods, so the period of total darkness was marked by the remaining 12 decan stars, resulting in the 12 divisions of the night. The time between the appearance of each of these decan stars over the horizon during the night would have been about 40 modern minutes. During the New Kingdom, the system was simplified, using a set of 24 stars, 12 of which marked the passage of the night.2

Not exactly an intuitive way to break time into smaller units, but evidently pervasive enough to be considered as a standard.  By the way, “decan” as used above appears to be derived from astrology (!) indicating a time of about 10 days between first rising.  The rest of this reference contains some mystery, since the Middle Kingdom of Egypt, which I believe is being referred to, is the 11^th through the 14^th dynasties, and ran roughly from 2055 BC to 1650 BC.  If this is the correct timeline, then, days divided into 12 or 24 has been around a while.

We saw, in an earlier post, that Ptolemy gets credit for breaking the degrees on his maps into minutes and seconds.  It seems likely that when the effort was made to subdivide hours, minutes and seconds were adapted.  Not too sure when, however, since “minutes” and “seconds” hands on clocks don’t show up until about the 15^th century, and their accuracy was questionable.

These are some apparent regularly repeating oscillations that could be starting points for calibration except for a few inconvenient facts about the main organ of calibration, the earth in relation to the sun, which raise some questions:

Question one: should the hours be equal all the time, or should daylight contain 12 hours and the nighttime 12 hours, whether it is summer or winter?  Based on the earth’s position in its course around the sun, the angle of its axis of rotation, approximately 23.5 degrees, has the southern hemisphere more directly aimed at the sun or the northern hemisphere more directly aimed at the sun.  This leads to the sun being in the sky much longer in the summer in the northern hemisphere.  Should that daylight time be divided into 12 hours, the same as the shorter daylight days of winter?

We are used to all hours being the same length and knowing that the sun rises at an earlier or later hour throughout the year, but our answer is not the only answer that has been used.  Dividing daylight hours and nighttime hours into 12 of each was used as the standard answer for thousands of years, and only began to change in Europe as mechanical clocks became better at telling equal hours.

Question two: how do you accommodate for the fact that there are times during the year when the sun appears to move faster and times when the sun moves slower, and that it does not appear in exactly the same place at midday?  Using the elapse of 24 hours, which is the mean solar day would be difficult for calibration.  Over the course of the year, the sun at midday would appear in the pattern of an analemma.  See the following website for an adequate explanation of this:

http://www.perseus.gr/Astro-Solar-Analemma.htm

So, if you were trying to make sure you made a sighting of the sun at the exact highest point of the day on two consecutive days to establish the length of 24 hours, that would not be precise enough.  You might be able to do it by establishing the mean solar day, take the amount of time for each day and essentially average it.  But doing that too might be difficult – how can you tell if 24 hours today is not exactly the same as 24 hours two days ago?

Question three: If you decided to use the stellar background, you would run into a problem here as well.   The mean solar day is approximately 24 hours long.  The sidereal day (based on the rotation of the earth relative to the stars) is approximately 23 hours and 56 minutes long.  Why is that?  Over the course of a year, any reference star that you chose would reappear in exactly the same spot, relative to the earth, approximately 365 (365.2422 more precisely) days later.  In between, each day, it would arrive at the same spot a little bit earlier, by 3 minutes and 56 seconds.  That is very close to the difference of one degree per day, which makes sense with a 365 day year.  If it advances just a shade under a degree per day, the sum of all of those is 360 degrees in 365 days.  But that makes the calibration difficult as well.

There are some additional cycles that could be looked at, but either their period is too long (26,000 year precession) to be practical, or doesn’t line up quite right over the course of a day, such as the moon.  It would be possible to base a calendar on the moon’s reappearance in exactly the same spot, relative to the earth and the sun, which takes about 29.5 days, but it doesn’t evenly divide into 365.2422.  (365.2422 / 29.5 = 12.3811)  Even trying to set up a clock based on the tides, affected by the moon, would run into inconsistency problems.

With this information before us, we are now able to determine that there is no way to calibrate a second.  Right?

If the story by Vincenzo Viviani is correct, Galileo realized that the period of the swing of a pendulum was pretty close to equal from swing to swing.  The tale has him realizing it while noting the swinging of a chandelier in the cathedral in Pisa, probably in a service that was the usual boring service.  An active mind searching for things to occupy it might just have noticed the swinging, put a finger on the wrist to feel the pulse, and made the realization.  While I may be projecting my own activities during that sort of situation, the story goes on to describe the use of a plumb line with a bob to understand the details of the insight more.  When he found the formula that describes the period as being proportional to the square root of the length of the pendulum, it would not be too difficult to imagine trying to find a pendulum length that was close to one second long.  But to do so, you would have to have some idea of how long a second is.

Timekeeping devices, while initially based or calibrated on the sky, had been brought down to earth by Egyptians, Babylonians, Chinese and Greeks, all of whom had versions of water clocks, or clypsydrae (singular: clypsydra).  Other devices to employ the same or similar means (material being removed from a container by gravity or fire) were candle clocks, incense clocks and sand hour clocks.  Sand hour clocks, also known as hour glasses could be made fairly precise by either adding or removing a little bit of sand after determining the right amount of time for an hour: if twenty-four were made with equal volumes of sand, and one turned over as soon as the last one finished in succession for a day, presumably one could start as the sun reached its highest point and the last of the 24 would just be emptied as the sun reached its highest point on the next day.  (It could probably be done with one hourglass turned over 24 times?)  This could be repeated until, by adding or removing a few grains of sand, it made the hour glasses pretty close to accurate.  In fact, it turns out, Magellan, when his fleet circumnavigated the globe in 1522, had eighteen hourglasses on each ship.

This would at least give a fairly accurate version of one hour.  Now, to subdivide that into minutes and seconds wouldn’t be too complicated.  Set up a pendulum that is the length you think is a second, start it swinging at the same time as you turn over an hourglass, and count to 3600 (60 X 60).  Too hard?  Well, in the 17^th century, a Jesuit, ‘…Father Giovanni Batista Ricciolli persuaded nine fellow Jesuits “to count nearly 87,000 oscillations in a single day.”‘3 3600 seconds in an hour times 24 hours is 86,400, so knowing Father Ricciolli’s reputation as a scientist, my guess is that the group would be broken into four groups of two, and each of the two would be responsible for their own count, which could be compared later.  They would rotate the shifts of counting.  That’s a guess, but the ability to do this, figure out that the pendulum was too long or too short, adjust it, try again might be an activity that would be used to calibrate the correct length, which it turns out is about a meter, or 39. 37 inches.

The first pendulum clock was designed and commissioned by Christiaan Huygens in 1656.  This clock and those made shortly thereafter increased the accuracy of mechanical clocks from about 15 minutes a day to about 15 seconds per day.  In 1671, Jean Richer took a pendulum clock that was accurate in Paris to Cayenne, French Guiana and discovered that it was 2.5 minutes per day slower.  His conclusion as to why was that gravity was not as strong in French Guiana.  A few years later, Newton speculated that due to the effect of centrifugal force on the rotation of the earth, there was a bulge at the equator and the poles were flattened.  The Cassinis of the French Royal Observatory disagreed, and a result was the trip to Peru to measure the shape of the earth.  So we are now almost to the point where we can answer the questions raised at the beginning of the post: how did the French workers go about calibrating their pendulum clocks?

Among the factors that affect the operation of a pendulum clock are gravity and temperature.  If the density of the material under the pendulum is high, as it would be under mountains, this will raise the gravity, thus speeding pendulums up a bit.  The opposite effect, that of Cayenne, also affects the rate of oscillation of pendulums.  Temperature can affect pendulums: Huygens used a solid rod for his pendulums, instead of a string or something similarly flexible, since the flex in flexible pendulums caused erratic swing periods.  But with a solid rod, heat can lengthen the rod, and cold cause it to contract, lengthening or shortening the period of its swing.  With these known factors potentially at play, a clock with a pendulum that had a one second period when it was taken to Quito, Peru, what would be the effect?  Depends on the density underneath, and the temperature.  By the time the French left for South America in 1735, at least two solutions to the temperature had been developed, and possibly a third.  However, from my research, I cannot tell if any of these had been employed in their pendulum clocks.

Presumably, they would have tried to control for temperature, and then assume that the differences would be a result of gravity.  So once with their calibrated-for-Paris clocks they had measured whether their clocks were slower or faster than the mean solar time in a few consecutive days, and used the result in two ways: one, to estimate the force of gravity beneath the clocks, and second, how much longer or shorter to set the pendulum to match 86,400 seconds to the time between two solar meridian crossings.  I’m certain that the amount of time their task took was lengthened by repeated calibrations.

There was an alternative that might have been used, but I cannot tell if they used it.  By the time they left, the transit of the moons of Jupiter had been precisely timed: when several of the moons went behind Jupiter and reappeared had been timed precisely enough that one astronomer, Ole Roemer in 1676, had proved that the speed of light was finite using the occultation of Io, one of Jupiter’s moons.  He timed the occultation when the earth in its orbit was nearer to Jupiter, then when earth was at a different part of its orbit, much further from Jupiter, and noted that the times of occultation took much longer when the earth was farther from Jupiter.  This he correctly assumed was because the distance was so much greater, and reasoned that because of that, light had a finite speed and was not infinitely fast.

Having precise timings for the transits or occultations of the Jovian moons meant that the French could have matched the seconds of their pendulum clocks to the amount of time for a transit or occultation, and adjust the clocks to match the standard timing.  Did they do that?  I don’t know for sure, but my guess is that they would have tried that in addition to meridian crossings by the sun.  They were well trained in the astronomical tasks of the day, so I’m sure that they would have tried any and possibly all methods available to them to establish the accuracy of their clocks, to insure the accuracy of their surveys.

The process of calibrating a pendulum clock, then, is not very straight forward.  At best it is an iterative process: check the timing against a known oscillation, if it is not correct, make a correction in the length of the pendulum that should either speed up the period or slow it down to match the known timing device, check it again.  If it is not correct, repeat until it is.

Choosing the reference oscillation is the key.  Pendulums were used to establish the standard until quartz oscillations were built into quartz clocks and then watches.  Now, the standard is based on the oscillations of cesium atoms in cesium clocks, and hydrogen oscillations in hydrogen maser clocks.  They are well beyond the accuracy of pendulum clocks.  The arrangement at the Naval Observatory is a Master Clock fed information by a set of cesium and hydrogen masers, which corrects itself based on the inputs.  The Master Clock “…keeps time to within one hundred picoseconds – one hundred trillionths of a second – over the course of each day, every day.  Had it been set when the dinosaurs went extinct, 60 million years ago, it would have gained or lost no more than about two seconds.”4

---

1 Herodotus, The Histories, Penguin Books, London, England.  Translated by Aubrey de Selincourt, 1954. Revised edition, 1972.  Revised edition with new introductory matter and notes by John Marincola 1996, further revision 2003. P. 96.  I had found so many “measurement” references to Herodotus that I bought a copy and am reading it.  Since Herodotus died around 425 and 420 BC, the book is surprisingly lively for 2400 years old.

2 http://en.wikipedia.org/wiki/Hour

3 http://en.wikipedia.org/wiki/History_of_timekeeping_devices

4 Falk, Dan, In Search of Time, The Science of a Curious Dimension, Thomas Dunn Books, St. Martin’s Press, New York, N.Y. 2008. p.56.  Full of good information and really poor proofreading.